Advertisements
Advertisements
प्रश्न
Find the distance between the origin and the point:
(-5, -12)
उत्तर
Coordinates of origin are O (0, 0).
B (-5, -12)
BO = `sqrt((0 + 5)^2 + (0 + 12)^2)`
= `sqrt(25 + 144)`
= `sqrt(169)`
= 13
APPEARS IN
संबंधित प्रश्न
If the point A(0, 2) is equidistant from the points B(3, p) and C(p, 5), find p. Also, find the length of AB.
Name the type of quadrilateral formed, if any, by the following point, and give reasons for your answer:
(−3, 5), (3, 1), (0, 3), (−1, −4)
Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (−3, 4).
If a≠b≠0, prove that the points (a, a2), (b, b2) (0, 0) will not be collinear.
Find the circumcenter of the triangle whose vertices are (-2, -3), (-1, 0), (7, -6).
Show that the ▢PQRS formed by P(2, 1), Q(–1, 3), R(–5, –3) and S(–2, –5) is a rectangle.
Find the distance between the following pairs of point in the coordinate plane :
(7 , -7) and (2 , 5)
Find the distance of the following point from the origin :
(0 , 11)
Find the relation between x and y if the point M (x,y) is equidistant from R (0,9) and T (14 , 11).
Find the coordinate of O , the centre of a circle passing through A (8 , 12) , B (11 , 3), and C (0 , 14). Also , find its radius.
Prove that the points P (0, -4), Q (6, 2), R (3, 5) and S (-3, -1) are the vertices of a rectangle PQRS.
Find the distance of the following points from origin.
(a+b, a-b)
Use distance formula to show that the points A(-1, 2), B(2, 5) and C(-5, -2) are collinear.
Show that the quadrilateral with vertices (3, 2), (0, 5), (- 3, 2) and (0, -1) is a square.
If the distance between point L(x, 7) and point M(1, 15) is 10, then find the value of x
Show that the point (11, – 2) is equidistant from (4, – 3) and (6, 3)
The distance between the points (0, 5) and (–5, 0) is ______.
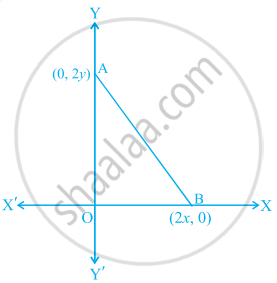
The coordinates of the point which is equidistant from the three vertices of the ΔAOB as shown in the figure is ______.
What type of a quadrilateral do the points A(2, –2), B(7, 3), C(11, –1) and D(6, –6) taken in that order, form?
