Advertisements
Advertisements
प्रश्न
Find the coordinate of O , the centre of a circle passing through A (8 , 12) , B (11 , 3), and C (0 , 14). Also , find its radius.
उत्तर
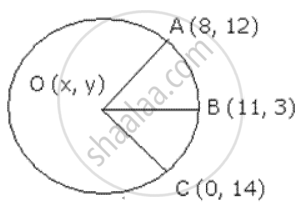
Let O (x , y) be the centre of the circle.
OA = OB (radii of the same circle)
⇒ OA2 = OB2
(x - 8)2 + (y - 12)2 = (x - 11)2 + (y -3)2
⇒ x2 + 64 - 16x + y2 + 144 - 24y = x2 + 121 - 22x + y2 + 9 - 6y
⇒ 6x - 18y + 78 = 0
⇒ x - 3y + 13 = 0
similarly , OB = OC
∴ OB2 = OC2
(x - 11)2 + (y - 3)2 = (x - 0)2 + (y - 14)2
⇒ x2 + 121 - 22x + y2 + 9 - 6y = x2 + y2 + 196 - 28y
⇒ - 22 x + 22 y - 66 = 0
⇒ - x + y - 3 =0 ..........(2)
x - 3y + 13 = 0 ..........(1)
solving (1) & (2) we get ,
- 2 y + 10 = 0
⇒ y = 5
from (1)
x - 15 + 13 = 0
⇒ x = 2
Thus , coordinates of O are (2,5)
Radius = `sqrt ((2 - 8)^2 + (5 - 12)^2) = sqrt (36 + 49) = sqrt 85` units
APPEARS IN
संबंधित प्रश्न
The value of 'a' for which of the following points A(a, 3), B (2, 1) and C(5, a) a collinear. Hence find the equation of the line.
Given a line segment AB joining the points A(–4, 6) and B(8, –3). Find
1) The ratio in which AB is divided by y-axis.
2) Find the coordinates of the point of intersection.
3) The length of AB.
Find the distance between the following pair of points:
(a+b, b+c) and (a-b, c-b)
Show that the quadrilateral whose vertices are (2, −1), (3, 4) (−2, 3) and (−3,−2) is a rhombus.
Find the distance between the points
(ii) A(7,-4)and B(-5,1)
Find the distance of a point (12 , 5) from another point on the line x = 0 whose ordinate is 9.
Prove that the points (5 , 3) , (1 , 2), (2 , -2) and (6 ,-1) are the vertices of a square.
In what ratio does the point P(−4, y) divides the line segment joining the points A(−6, 10) and B(3, −8)? Hence find the value of y.
Find distance between point A(–1, 1) and point B(5, –7):
Solution: Suppose A(x1, y1) and B(x2, y2)
x1 = –1, y1 = 1 and x2 = 5, y2 = – 7
Using distance formula,
d(A, B) = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`
∴ d(A, B) = `sqrt(square +[(-7) + square]^2`
∴ d(A, B) = `sqrt(square)`
∴ d(A, B) = `square`
If (– 4, 3) and (4, 3) are two vertices of an equilateral triangle, find the coordinates of the third vertex, given that the origin lies in the interior of the triangle.
