Question

Find the coordinate of O , the centre of a circle passing through A (8 , 12) , B (11 , 3), and C (0 , 14). Also , find its radius.

Answer 1

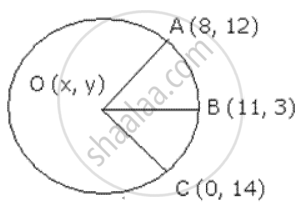
Let O (x , y) be the centre of the circle.

OA = OB (radii of the same circle)

⇒ OA² = OB²

(x - 8)² + (y - 12)² = (x - 11)² + (y -3)²

⇒ x² + 64 - 16x + y² + 144 - 24y = x² + 121 - 22x + y² + 9 - 6y 

⇒ 6x - 18y + 78 = 0

⇒ x - 3y + 13 = 0

similarly , OB = OC 

∴ OB² = OC²

(x - 11)² + (y - 3)² = (x - 0)² + (y - 14)²

⇒ x² + 121 - 22x + y² + 9 - 6y = x² + y² + 196 - 28y 

⇒ - 22 x + 22 y - 66 = 0

⇒ - x + y - 3 =0      ..........(2)

x - 3y + 13 = 0        ..........(1)

solving (1) &  (2) we get ,

- 2 y + 10 = 0

⇒ y = 5

from (1)

x - 15 + 13 = 0

⇒ x = 2

Thus , coordinates of O are (2,5)

Radius = `sqrt ((2 - 8)^2 + (5 - 12)^2) = sqrt (36 + 49) = sqrt 85` units