Question

Find the coordinate of O , the centre of a circle passing through P (3 , 0), Q (2 , `sqrt 5`) and R (`-2 sqrt 2` , -1). Also find its radius.

Answer 1

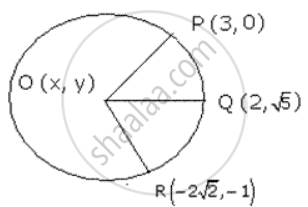
Let O (x, y) be the centre of the circle

OP = OQ (radii of same circle)

⇒ OP² = OQ²

`(sqrt (("x" - 3)^2 + ("y" - 0)^2))^2 = (sqrt (("x" - 2)^2 + ("y" - sqrt 5)^2))^2`

⇒ x² + 9 - 6x + y² = x² + 4 - 4x + y² + 5 - 2`sqrt 5`y

⇒ - 2x + 2`sqrt 5`y = 0

⇒ - x + `sqrt 5` y = 0    .........(1)

Similarly , OQ = OR

⇒  OQ² = OR²

⇒ (x - 2)² + (y - `sqrt 5`)² = (x + 2 `sqrt 2`)²  + (y + 1)²

⇒ x² + 4 - 4x + y² + 5 - 2`sqrt 5` y = x² + 8 + `4 sqrt 2` + y² + 1 + 2y

⇒ - 4 x - `4sqrt 2 "x" - 2 sqrt 5 "y" = 0`

⇒ - 2x - 2`sqrt 2 "x"` - `sqrt 5 "y"` - y = 0 .......(2)

Putting x = `sqrt 5` y from (1) and (2)

`-2 sqrt 5 "y" - 2 sqrt 10 "y" - sqrt 5 "y" - "y" = 0`

`(-3sqrt 5 - 2sqrt 10 - 1) "y" = 0`

y = 0

from (1)

x = `sqrt 5 (0) = 0`

⇒ x = 0

Thus , coordinates of O are (0 , 0).

Radius = `sqrt ((0-3)^2 + (0 - 0)^2) = sqrt 9` = 3 units