Advertisements
Advertisements
प्रश्न
Find the coordinate of O , the centre of a circle passing through P (3 , 0), Q (2 , `sqrt 5`) and R (`-2 sqrt 2` , -1). Also find its radius.
उत्तर
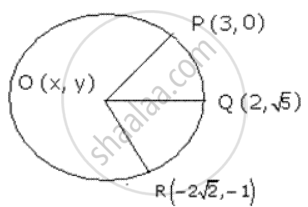
Let O (x, y) be the centre of the circle
OP = OQ (radii of same circle)
⇒ OP2 = OQ2
`(sqrt (("x" - 3)^2 + ("y" - 0)^2))^2 = (sqrt (("x" - 2)^2 + ("y" - sqrt 5)^2))^2`
⇒ x2 + 9 - 6x + y2 = x2 + 4 - 4x + y2 + 5 - 2`sqrt 5`y
⇒ - 2x + 2`sqrt 5`y = 0
⇒ - x + `sqrt 5` y = 0 .........(1)
Similarly , OQ = OR
⇒ OQ2 = OR2
⇒ (x - 2)2 + (y - `sqrt 5`)2 = (x + 2 `sqrt 2`)2 + (y + 1)2
⇒ x2 + 4 - 4x + y2 + 5 - 2`sqrt 5` y = x2 + 8 + `4 sqrt 2` + y2 + 1 + 2y
⇒ - 4 x - `4sqrt 2 "x" - 2 sqrt 5 "y" = 0`
⇒ - 2x - 2`sqrt 2 "x"` - `sqrt 5 "y"` - y = 0 .......(2)
Putting x = `sqrt 5` y from (1) and (2)
`-2 sqrt 5 "y" - 2 sqrt 10 "y" - sqrt 5 "y" - "y" = 0`
`(-3sqrt 5 - 2sqrt 10 - 1) "y" = 0`
y = 0
from (1)
x = `sqrt 5 (0) = 0`
⇒ x = 0
Thus , coordinates of O are (0 , 0).
Radius = `sqrt ((0-3)^2 + (0 - 0)^2) = sqrt 9` = 3 units
APPEARS IN
संबंधित प्रश्न
Show that the quadrilateral whose vertices are (2, −1), (3, 4) (−2, 3) and (−3,−2) is a rhombus.
Find value of x for which the distance between the points P(x,4) and Q(9,10) is 10 units.
Prove that the points (0,3) , (4,3) and `(2, 3+2sqrt 3)` are the vertices of an equilateral triangle.
Prove that the points (a, b), (a + 3, b + 4), (a − 1, b + 7) and (a − 4, b + 3) are the vertices of a parallelogram.
A point P lies on the x-axis and another point Q lies on the y-axis.
Write the abscissa of point Q.
The points A (3, 0), B (a, -2) and C (4, -1) are the vertices of triangle ABC right angled at vertex A. Find the value of a.
The distance between points P(–1, 1) and Q(5, –7) is ______
Show that A(1, 2), (1, 6), C(1 + 2 `sqrt(3)`, 4) are vertices of a equilateral triangle
The point A(2, 7) lies on the perpendicular bisector of line segment joining the points P(6, 5) and Q(0, – 4).
The point P(–2, 4) lies on a circle of radius 6 and centre C(3, 5).
