Advertisements
Advertisements
Question
Prove that the straight line joining the vertex of an isosceles triangle to any point in the base is smaller than either of the equal sides of the triangle.
Solution
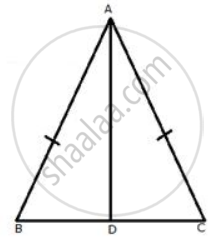
We know that the exterior angle of a triangle is always greater than each of the interior opposite angles.
∴ In ΔABD,
∠ADC > ∠B ...(i)
In ΔABC,
AB = AC
∴∠B = ∠C ...(ii)
From (i) and (ii)
∠ADC > ∠C
(i) In ΔADC,
∠ADC > ∠C
∴AC > AD ....(iii)[ side opposite to greater angle is greater ]
(ii) In ΔABC,
AB = AC
⇒ AB > AD ...[ From (iii) ]
APPEARS IN
RELATED QUESTIONS
The sides AB and AC of a triangle ABC are produced; and the bisectors of the external angles at B and C meet at P. Prove that if AB > AC, then PC > PB.
In the following figure, ABC is an equilateral triangle and P is any point in AC;
prove that: BP > PA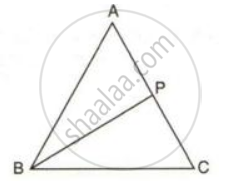
From the following figure; 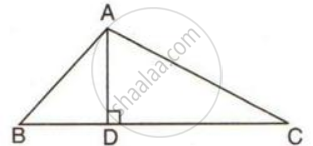
prove that:
(i) AB > BD
(ii) AC > CD
(iii) AB + AC > BC.
