Advertisements
Advertisements
Question
In the following diagram; AD = AB and AE bisect angle A. 
Prove that:
(i) BE = DE
(ii) ∠ABD > ∠C
Solution
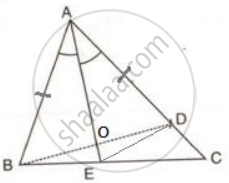
Const: Join ED.
In ΔAOB and ΔAOD,
AB = AD ...[ Given ]
AO = AO ....[ Common ]
∠BAO = ∠DAO ....[ AO is bisector of A ]
∴ ΔAOB ≅ ΔAOD ....[ SAS criterion ]
Hence,
BO = OD …(i)[ c.p.c.t. ]
∠AOB = ∠AOD …(ii)[ c.p.c.t. ]
∠ABO = ∠ADO ⇒ ∠ABD = ∠ADB …(iii)[ c.p.c.t. ]
Now,
∠AOB = ∠DOE ...[Vertically opposite angles]
∠AOD = ∠BOE ...[Vertically opposite angles]
∠BOE = ∠DOE …(iv)[ From (ii) ]
(i) In ΔBOE and ΔDOE,
BO = OD ...[ From (i) ]
OE = OE ...[ Common ]
∠BOE = ∠DOE ...[ From (iv) ][ SAS criterion ]
Hence, BE = DE ...[ c.p.c.t. ]
(ii) In BCD,
∠ADB = ∠C + ∠CBD ...[ Ext. angle = sum of opp. int. angles ]
⇒ ∠ADB > ∠C
⇒ ∠ABD > ∠C ...[ From (iii) ]
APPEARS IN
RELATED QUESTIONS
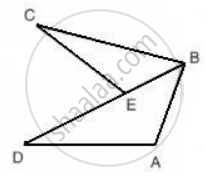
In triangle ABC, AB > AC and D is a point inside BC.
Show that: AB > AD.
Given: ED = EC
Prove: AB + AD > BC.
In an isosceles triangle ABC, sides AB and AC are equal. If point D lies in base BC and point E lies on BC produced (BC being produced through vertex C), prove that:
(i) AC > AD
(ii) AE > AC
(iii) AE > AD
In triangle ABC, side AC is greater than side AB. If the internal bisector of angle A meets the opposite side at point D,
prove that: ∠ADC is greater than ∠ADB.
In quadrilateral ABCD, side AB is the longest and side DC is the shortest.
Prove that: C > A.
In quadrilateral ABCD, side AB is the longest and side DC is the shortest.
Prove that: D > B.
In the following figure; AB is the largest side and BC is the smallest side of triangle ABC.
Write the angles xo, yo and zo in ascending order of their values.
P is any point inside the triangle ABC.
Prove that: ∠BPC > ∠BAC.
In the following figure, ABC is an equilateral triangle and P is any point in AC;
prove that: BP > PC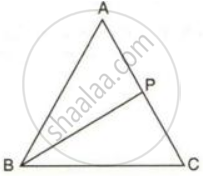
In a quadrilateral ABCD; prove that:
(i) AB+ BC + CD > DA
(ii) AB + BC + CD + DA > 2AC
(iii) AB + BC + CD + DA > 2BD
