Advertisements
Advertisements
Question
In a quadrilateral ABCD; prove that:
(i) AB+ BC + CD > DA
(ii) AB + BC + CD + DA > 2AC
(iii) AB + BC + CD + DA > 2BD
Solution

Const: Join AC and BD.
(i) In ΔABC,
AB + BC > AC ….(i)[ Sum of two sides is greater than the third side ]
In ΔACD,
AC + CD > DA ….(ii)[ Sum of two sides is greater than the third side ]
Adding (i) and (ii)
AB + BC + AC + CD > AC + DA
AB + BC + CD > AC + DA - AC
AB + BC + CD > DA ….(iii)
(ii) In ΔACD,
CD + DA > AC ….(iv) [Sum of two sides is greater than the third side]
Adding (i) and (iv)
AB + BC + CD + DA > AC + AC
AB + BC + CD + DA > 2AC
(iii) In ΔABD,
AB + DA > BD ….(v)[Sum of two sides is greater than the third side]
In ΔBCD,
BC + CD > BD ….(vi)[Sum of two sides is greater than the third side]
Adding (v) and (vi)
AB + DA + BC + CD > BD + BD
AB + DA + BC + CD > 2BD
APPEARS IN
RELATED QUESTIONS
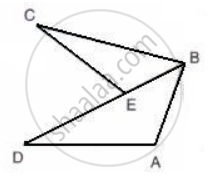
In triangle ABC, AB > AC and D is a point inside BC.
Show that: AB > AD.
Given: ED = EC
Prove: AB + AD > BC.
In an isosceles triangle ABC, sides AB and AC are equal. If point D lies in base BC and point E lies on BC produced (BC being produced through vertex C), prove that:
(i) AC > AD
(ii) AE > AC
(iii) AE > AD
In triangle ABC, side AC is greater than side AB. If the internal bisector of angle A meets the opposite side at point D,
prove that: ∠ADC is greater than ∠ADB.
In quadrilateral ABCD, side AB is the longest and side DC is the shortest.
Prove that: C > A.
In quadrilateral ABCD, side AB is the longest and side DC is the shortest.
Prove that: D > B.
In the following figure; AB is the largest side and BC is the smallest side of triangle ABC.
Write the angles xo, yo and zo in ascending order of their values.
In the following diagram; AD = AB and AE bisect angle A. 
Prove that:
(i) BE = DE
(ii) ∠ABD > ∠C
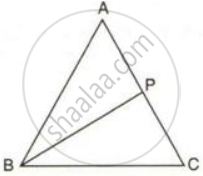
P is any point inside the triangle ABC.
Prove that: ∠BPC > ∠BAC.
In the following figure, ABC is an equilateral triangle and P is any point in AC;
prove that: BP > PC