Question

Prove that under certain conditions a magnet vibrating in a uniform magnetic field performs angular S.H.M.

Answer 1

If a bar magnet is freely suspended in the plane of a uniform magnetic field, it remains in equilibrium with its axis parallel to the direction of the field. If it is given a small angular displacement θ (about an axis passing through its centre, perpendicular to itself and to the field) and released, it performs angular oscillations.

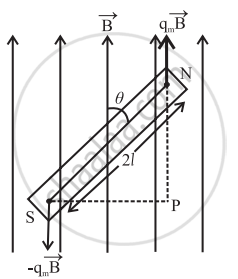
Let µ be the magnetic dipole moment and B the magnetic field. In the deflected position, a restoring torque acts on the magnet, which tends to bring it back to its equilibrium position. [Here we used the symbol µ for the magnetic dipole moment as the symbol m is used for mass].

The magnitude of this torque is τ = µ B sin θ

If θ is small, sin θ ≅ θ^c    ∴ τ = µBθ

For clockwise angular displacement θ , the restoring torque is in the anticlockwise direction.

∴ τ = Iα = - µBθ

where I is the moment of inertia of the bar magnet and α is its angular acceleration.

`therefore alpha = - ((mu"B")/"I")theta`   ...(i)

Since µ, B and I are constants, Eq. (i) shows that angular acceleration is directly proportional to the angular displacement and directed opposite to the angular displacement. Hence the magnet performs angular S.H.M. The period of vibrations of the magnet is given by

T = `(2pi)/sqrt("angular acceleration per unit  angular displacement")`

`= (2pi)/sqrt(alpha/theta)`

`therefore "T" = 2pi sqrt("I"/(mu"B"))`