Question

परवलय x² = 4y और वृत्त 4x² + 4y² = 9 के मध्यवर्ती क्षेत्र का क्षेत्रफल ज्ञात कीजिए।

Answer 1

परवलय का समीकरण x² = 4y …(i)

तथा वृत्त का समीकरण x² + y² `= (3/2)^2` …(ii)

समीकरण (i) व (ii) को हल करने पर बिंदु `(pm sqrt2, 1/2)` प्रतिच्छेदन बिंदु के रूप में प्राप्त होते हैं।

∴ दोनों वक्र x-अक्ष के सममित हैं।

∴ अभीष्ट क्षेत्रफल = 2 × ODCAO का क्षेत्रफल

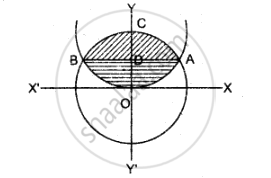
= 2 x (ODAO का क्षेत्रफल + CAD का क्षेत्रफल)

`= 2 int_0^(1//2)  "dy" + 2 int_(1//2)^(3//2) x" dy"` (वृत्त)

`= 2 int_0^(1//2) 2sqrt"y"  "dx" + 2 int_(1//2)^(3//2)  sqrt(9/4 - "y"^2) "dy"`

`= 4 xx 2/3  ("y"^(3//2))_0^(3//2) + 2["y"/2 sqrt((9/4) - "y"^2) + 9/8  sin^-1  (2"y")/3]_(1//2)^(3//2)`

`= 8/3 (1/(2sqrt2) - 0) + [{9/4  sin^-1  (1)} - {sqrt2/2 + 9/4  sin^-1  (1/3)}]`

`= 2 sqrt2/3 - sqrt2/2 + 9/4  (sin^-1 (1) - sin^-1  1/3)`

`= sqrt2/6 + 9/4  sin^-1  (1. (2sqrt2)/6 - 0)`

`= [sqrt2/6 + 9/4  sin^-1  ((2sqrt2)/3)]`  वर्ग इकाई