Advertisements
Advertisements
Question
Represent the number `sqrt(7)` on the number line.
Solution
Let us find `sqrt(5)`.
Draw a number line.
Mark a point O representing zero.
Take point A on number line such that OA = 2
Construct AB ⊥ OA such that AB = 1 unit.
∴ ΔOAB is a right triangle.
In ΔOAB, (OB)2 = (OA)2 + (AB)2 (Pythagoras' Theorem)
∴ (OB)2 = 22 + 12
∴ (OB)2 = 5
⇒ OB = `sqrt(5)`
Now, let us find `sqrt(6)`.
Construct BC ⊥ OB, such that BC = 1 unit.
∴ ΔOBC is a right triangle.
In ΔOBC, OC2 = OB2 + BC2 (Pythagoras' Theorem)
∴ OC2 = `(sqrt(5))^2 + 1^2`
∴ OC2 = 6
⇒ OC = `sqrt(6)`
Now, let us find `sqrt(7)`.
Construct CD ⊥ OC, such that CD = 1 unit.
In ΔOCD, OD2 = OC2 + CD2 (Pythagoras' Theorem)
∴ OD2 = `(sqrt(6))^2 + 1^2`
∴ OD2 = 7
⇒ `sqrt(7)`
Draw an arc of radius OD and centre O and let it intersect the number line at point E.
∴ `sqrt(7)` is thus marked at point E on the number line.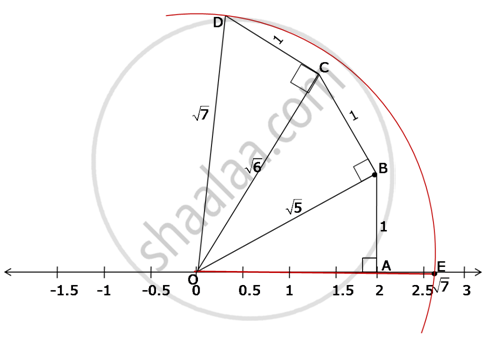
APPEARS IN
RELATED QUESTIONS
Find two irrational numbers lying between 0.1 and 0.12.
Which of the following statements is true?
Write a pair of irrational numbers whose difference is rational.
Check whether the square of the following is rational or irrational:
`sqrt(2) + sqrt(3)`
Show that `sqrt(5)` is an irrational numbers. [Use division method]
`(6 + 5sqrt3) - (4 - 3 sqrt3)` is ______.
Prove that `sqrt(3) + sqrt(5)` is irrational.
Classify the following number as rational or irrational with justification:
`- sqrt(0.4)`
Insert a rational number and an irrational number between the following:
`(-2)/5` and `1/2`
Prove that `sqrt(5)` is an irrational number.
