Advertisements
Advertisements
Question
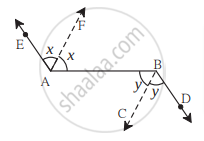
रेषा AB व रेषा CD या रेषांना रेषा EF ही अनुक्रमे P व Q बिंदूंत छेदते. किरण PR व किरण QS हे समांतर किरण असून अनुक्रमे ∠BPQ व ∠PQC चे दुभाजक आहेत, तर सिद्ध करा रेषा AB || रेषा CD.

Sum
Solution
किरण PR व किरण QS हे समांतर किरण असून अनुक्रमे ∠BPQ व ∠PQC चे दुभाजक आहेत, म्हणून
∠RPQ = ∠RPB = `1/2`∠BPQ आणि ∠SQP = ∠SQC = `1/2`∠PQC
∴ ∠BPQ = 2∠RPQ आणि ∠PQC = 2∠SQP ...(1)
किरण PR || किरण QS व रेख PQ ही त्यांना P आणि Q वर छेदणारी छेदिका आहे.
∠RPQ = ∠SQP ...(आंतरव्युत्क्रम कोन)
दोन्ही बाजूंना 2 ने गुणून
2∠RPQ = 2∠SQP
∴ (1) वरून
∠BPQ = ∠PQC
परंतु, ∠BPQ आणि ∠PQC हे रेषा AB आणि रेषा CD वरील छेदिका EF द्वारे निर्मित आंतरव्युत्क्रम कोन आहेत.
∴ रेषा AB || रेषा CD ...(व्युत्क्रम कोन कसोटी)
shaalaa.com
रेषांच्या समांतरतेच्या कसोट्या
Is there an error in this question or solution?