Advertisements
Advertisements
Question
Rod AB of length 3 m is kept on a smooth plane as shown in the given figure.The velocity of end A is 5 m/s along the inclined plane.Locate the ICR and find velocity of end B.
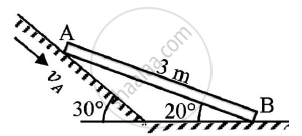
Given : Length of rod AB = 3m
va = 5 m/s
To find: ICR
Velocity of end B
Solution 1
Solution :

Given : AB = 3m
vA =5m /s
To find : ICR
vB
Solution:
ICR is shown in the diagram denoted by point I
Assume ω to be the angular velocity of rod AB
BY GEOMETRY:
∠CAD=30o, ∠ABD=20o
∠CAB= ∠ABD=20o
∠CAI=90o-30o
=60o
∠BAI = ∠CAI+ ∠CAB=60o+20o
=80o
In △IAB. ∠AIB = 180o-80o-70o
=30o
BY SINE RULE :
`(AB)/(sin I) =(IB)/(sin A )=(IA)/(sin B)`
`3/(sin 30) = (IB)/(sin 80 ) = (IA)/(sin 70)`
IB=5.9088 m
IA=5.6382 m
`ω = (v_a)/r = (v_a)/(IA) = 5/(5.6382)` = 0.8868 rad/s(anti clockwise)
vB = r ω
= IB x ω
= 5.9088 x 0.8868
=5.2401 m/s (Towards right)
Velocity of end B=5.2401 m/s (towards right)
Solution 2
Given : Length of rod AB = 3m
va = 5 m/s
To find: ICR
Velocity of end B
Solution :

Given : AB = 3m
vA =5m /s
To find : ICR
vB
Solution:
ICR is shown in the diagram denoted by point I
Assume ω to be the angular velocity of rod AB
BY GEOMETRY:
∠CAD=30o, ∠ABD=20o
∠CAB= ∠ABD=20o
∠CAI=90o-30o
=60o
∠BAI = ∠CAI+ ∠CAB=60o+20o
=80o
In △IAB. ∠AIB = 180o-80o-70o
=30o
BY SINE RULE :
`(AB)/(sin I) =(IB)/(sin A )=(IA)/(sin B)`
`3/(sin 30) = (IB)/(sin 80 ) = (IA)/(sin 70)`
IB=5.9088 m
IA=5.6382 m
`ω = (v_a)/r = (v_a)/(IA) = 5/(5.6382)` = 0.8868 rad/s(anti clockwise)
vB = r ω
= IB x ω
= 5.9088 x 0.8868
=5.2401 m/s (Towards right)
Velocity of end B=5.2401 m/s (towards right)
APPEARS IN
RELATED QUESTIONS
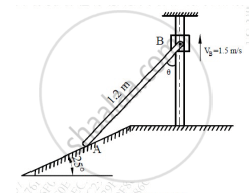
Using Instantaneous Centre of Rotation (ICR) method, find the velocity of point A for the instant shown in Figure 2. Collar B moves along the vertical rod, whereas link AB moves along the plane which is inclined at 250. Ɵ = 450
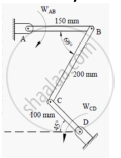
The link CD of the mechanism shown in Figure 7 is rotating in counterclockwise direction at an angular velocity of 5 rad/s. For the given instance, determine the angular velocity of link AB.