Advertisements
Advertisements
Question
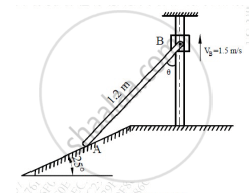
Using Instantaneous Centre of Rotation (ICR) method, find the velocity of point A for the instant shown in Figure 2. Collar B moves along the vertical rod, whereas link AB moves along the plane which is inclined at 250. Ɵ = 450
Solution
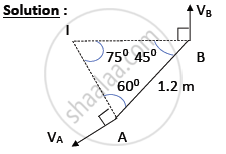
By using sine rule,
`(AB)/sinI = (BI)/sinA =( AI)/sin B`
`BI = (1.2 xx sin (60))/(sin (75)) = 1.076m`
`AI = (1.2 xx sin (45))/(sin (75)) = 0.878m`
ωAB = BI x VB = 1.076 x 1.5 = 1.614 rad/s
ωAB = AI x VA
`V_A =(omegaAB)/(AI) = 1.614/0.878 = 1.838`m/s
The velocity of point A for the given instance is 1.838 m/s.
APPEARS IN
RELATED QUESTIONS
Rod AB of length 3 m is kept on a smooth plane as shown in the given figure.The velocity of end A is 5 m/s along the inclined plane.Locate the ICR and find velocity of end B.
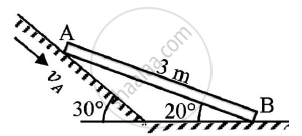
Given : Length of rod AB = 3m
va = 5 m/s
To find: ICR
Velocity of end B
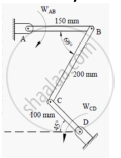
The link CD of the mechanism shown in Figure 7 is rotating in counterclockwise direction at an angular velocity of 5 rad/s. For the given instance, determine the angular velocity of link AB.