Advertisements
Advertisements
Question
Show that the line segments joining the mid-points of opposite sides of a quadrilateral bisects each other.
Solution
Let ABCD is the quadrilateral and P, Q, R, S are mid points of the sides AB, BC, CD, DA respectively.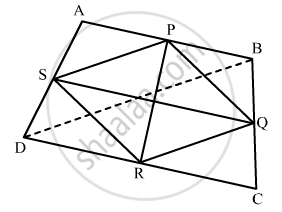
Join DB to form triangle ABD.
\[\frac{AS}{SD} = \frac{AP}{PB}\]
\[ \Rightarrow SP || DB \hspace{0.167em} \hspace{0.167em} and \hspace{0.167em} \hspace{0.167em} SP = \frac{1}{2} \hspace{0.167em} DB\]
In triangle BCD
\[\frac{CR}{RD} = \frac{CQ}{QB}\]
\[ \Rightarrow RQ || DB \hspace{0.167em} \hspace{0.167em} and \hspace{0.167em} \hspace{0.167em} RQ = \frac{1}{2} \hspace{0.167em} \hspace{0.167em} DB\]
In quadrilateral PQRS,
SP = RQ and SP || RQ
∴ PQRS is a parallelogram.
Diagonals of a parallelogram bisect each other.
∴ PR and QS bisect each other.
APPEARS IN
RELATED QUESTIONS
The two vectors `hatj+hatk " and " 3hati-hatj+4hatk` represent the two sides AB and AC, respectively of a ∆ABC. Find the length of the median through A
Find the position vector of a point R which divides the line joining the two points P and Q with position vectors \[\vec{OP} = 2 \vec{a} + \vec{b}\] and \[\vec{OQ} = \vec{a} - 2 \vec{b}\], respectively in the ratio 1 : 2 internally and externally.
Let \[\vec{a,} \vec{b,} \vec{c,} \vec{d}\] be the position vectors of the four distinct points A, B, C, D. If \[\vec{b} - \vec{a} = \vec{c} - \vec{d}\], then show that ABCD is a parallelogram.
If \[\vec{a,} \vec{b}\] are the position vectors of A, B respectively, find the position vector of a point C in AB produced such that AC = 3 AB and that a point D in BA produced such that BD = 2BA.
Show that the four points A, B, C, D with position vectors \[\vec{a,} \vec{b,} \vec{c,} \vec{d}\] respectively such that \[3 \vec{a} - 2 \vec{b} + 5 \vec{c} - 6 \vec{d} = 0,\] are coplanar. Also, find the position vector of the point of intersection of the line segments AC and BD.
Show that the four points P, Q, R, S with position vectors \[\vec{p}\], \[\vec{q}\], \[\vec{r}\], \[\vec{s}\] respectively such that 5 \[\vec{p}\] − 2 \[\vec{q}\] + 6 \[\vec{r}\] − 9 \[\vec{s}\] \[\vec{0}\], are coplanar. Also, find the position vector of the point of intersection of the line segments PR and QS.
If the position vector of a point (−4, −3) be \[\vec{a,}\] find \[\left| \vec{a} \right|\]
Find the coordinates of the tip of the position vector which is equivalent to \[\vec{A} B\], where the coordinates of A and B are (−1, 3) and (−2, 1) respectively.
If \[\vec{a}\] be the position vector whose tip is (5, −3), find the coordinates of a point B such that \[\overrightarrow{AB} =\] \[\vec{a}\], the coordinates of A being (4, −1).
Show that the points 2 \[\hat{i}, - \hat{i}-4 \] \[\hat{j}\] and \[-\hat{i}+4\hat{j}\] form an isosceles triangle.
If \[\overrightarrow{PQ} = 3 \hat{i} + 2 \hat{j} - \hat{k}\] and the coordinates of P are (1, −1, 2), find the coordinates of Q.
If the vertices of a triangle are the points with position vectors \[a_1 \hat{i} + a_2 \hat{j} + a_3 \hat{k} , b_1 \hat{i} + b_2 \hat{j} + b_3 \hat{k} , c_1 \hat{i} + c_2 \hat{j} + c_3 \hat{k} ,\]
what are the vectors determined by its sides? Find the length of these vectors.
Find the position vector of a point R which divides the line segment joining points \[P \left( \hat{i} + 2 \hat{j} + \hat{k} \right) \text{ and Q }\left( - \hat{i} + \hat{j} + \hat{k} \right)\] internally 2:1.
Find the position vector of a point R which divides the line segment joining points:
\[P \left( \hat{i} + 2 \hat{j} + \hat{k}\right) \text { and } Q \left( - \hat{i} + \hat{j} + \hat{k} \right)\] externally
Find the position vector of the mid-point of the vector joining the points P (2, 3, 4) and Q(4, 1, −2).
If \[\vec{a,} \vec{b}\] are two non-collinear vectors prove that the points with position vectors \[\vec{a} + \vec{b,} \vec{a} - \vec{b}\text{ and }\vec{a} + \lambda \vec{b}\] are collinear for all real values of λ.
If the points A(m, −1), B(2, 1) and C(4, 5) are collinear, find the value of m.
Show that the points whose position vectors are as given below are collinear:
\[2 \hat{i} + \hat{j} - \hat{k} , 3 \hat{i} - 2 \hat{j} + \hat{k} \text{ and }\hat{i} + 4 \hat{j} - 3 \hat{k}\]
Show that the points whose position vectors are as given below are collinear: \[3 \hat{i} - 2 \hat{j} + 4 \hat{k}, \hat{i} + \hat{j} + \hat{k}\text{ and }- \hat{i} + 4 \hat{j} - 2 \hat{k}\]
Show that the four points having position vectors
\[6 \hat{i} - 7 \hat{j} , 16 \hat{i} - 19 \hat{j} - 4 \hat{k} , 3 \hat{j} - 6 \hat{k} , 2 \hat{i} - 5 \hat{j} + 10 \hat{k}\] are coplanar.
Define position vector of a point.
If D is the mid-point of side BC of a triangle ABC such that \[\overrightarrow{AB} + \overrightarrow{AC} = \lambda \overrightarrow{AD} ,\] write the value of λ.
Find the image P' of the point P having position vector `hati+ 3hatj+ 4hatk` in the plane `vecr. (2hati - hatj + hatk) + 3 = 0 .` Hence find the length of PP'.
Find the position vector of the point which divides the join of points with position vectors `vec"a" + 3vec"b" and vec"a"- vec"b"` internally in the ratio 1 : 3.
X and Y are two points with position vectors `3vec("a") + vec("b")` and `vec("a")-3vec("b")`respectively. Write the position vector of a point Z which divides the line segment XY in the ratio 2 : 1 externally.
Find the value of x such that the four-point with position vectors,
`"A"(3hat"i"+2hat"j"+hat"k"),"B" (4hat"i"+"x"hat"j"+5hat"k"),"c" (4hat"i"+2hat"j"-2hat"k")`and`"D"(6hat"i"+5hat"j"-hat"k")`are coplaner.
Find the position vector of a point R which divides the line joining the two points P and Q with position vectors `vec"OP" = 2vec"a" + vec"b"` and `vec"OQ" = vec"a" - 2vec"b"`, respectively, in the ratio 1:2 internally
The position vector of the point which divides the join of points with position vectors `vec"a" + vec"b"` and 2`vec"a" - vec"b"` in the ratio 1:2 is ______.
The position vector of the point which divides the join of points `2vec"a" - 3vec"b"` and `vec"a" + vec"b"` in the ratio 3:1 is ______.
Position vector of the mid-point of line segment AB is `3hati + 2hatj - 3hatk`. If position vector of the point A is `2hati + 3hatj - 4hatk`, then position vector of the point B is ______.
