Advertisements
Advertisements
Question
Show the nature of the following graph for a satellite orbiting the earth.
- KE vs orbital radius R
- PE vs orbital radius R
- TE vs orbital radius R.
Solution
Consider the diagram, where a satellite of mass m, moves around the earth in a circular orbit of radius R.

The orbital speed of the satellite orbiting the earth is given by `v_0 = sqrt((GM)/R)` where M and R are the mass and radius of the earth.
a. ∴ KE of a satellite of mass m,
= `1/2 mv_0^2 `
= `1/2m xx (GM)/R`
∴ `E_k ∝ 1/R`
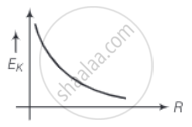
It means the KE decrease exponentially with radius. The graph for KE versus orbital radius R is shown in figure.
b. Potential energy of a satellite `E-p = - (GMn)/R`
`E_p ∝ 1/R`
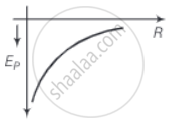
The graph for PE versus orbital radius R is shown in figure.
c. Total energy of the satellite `E = E_k + E_p`
= `(Gmm)/(2R) - (GMm)/R`
= `- (GMm)/(2R)`
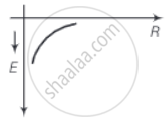
The graph for total energy versus orbital radius R is shown in the figure.
APPEARS IN
RELATED QUESTIONS
As the earth rotates about its axis, a person living in his house at the equator goes in a circular orbit of radius equal to the radius of the earth. Why does he/she not feel weightless as a satellite passenger does?
At what rate should the earth rotate so that the apparent g at the equator becomes zero? What will be the length of the day in this situation?
What is the true weight of an object in a geostationary satellite that weighed exactly 10.0 N at the north pole?
Answer the following question.
What is periodic time of a geostationary satellite?
Answer the following question in detail.
Obtain an expression for the binding energy of a satellite revolving around the Earth at a certain altitude.
The ratio of energy required to raise a satellite to a height `(2R)/3` above earth's surface to that required to put it into the orbit at the same height is ______.
R = radius of the earth
The period of revolution of a satellite is ______.
Is it possibe for a body to have inertia but no weight?
The ratio of binding energy of a satellite at rest on earth's surface to the binding energy of a satellite of same mass revolving around the earth at a height h above the earth's surface is ______ (R = radius of the earth).
A satellite is revolving around a planet in a circular orbit close to its surface and ρ is the mean density and R is the radius of the planet, then the period of ______.
(G = universal constant of gravitation)
