Question

ΔSHR ∼ ΔSVU, ΔSHR में SH = 4.5 सेमी, HR = 5.2 सेमी, SR = 5.8 सेमी तथा `"SH"/"SV" = 3/5` तो ΔSVU की रचना कीजिए।

Answer 1

कच्ची आकृति

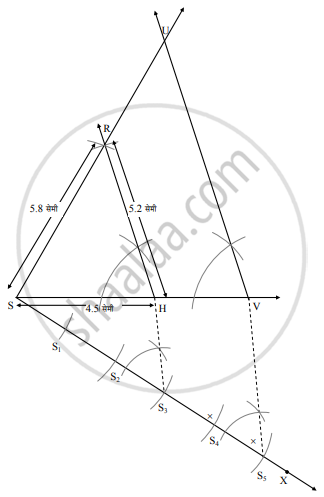
रचना के सोपान:

1. 4.5 सेमी लंबाईयों की एक रेख SH खींचिए।
2. बिंदु S से 5.8 सेमी लंबाई का एक चाप बनाएँ और बिंदु H से 5.2 सेमी लंबाई का चाप बनाएँ। उनके प्रतिच्छेदन बिंदु का नाम R रखें।
3. ΔRSH प्राप्त करने के लिए रेखा RS और रेखा RH को मिलाइए।
4. ∠HSX यह न्यूनकोण के लिए किरण SX खींचिए।
5. किरण SX पर बिंदु S₁, S₂, S₃, S₄, S₅ इस प्रकार लें जो SS₁ = S₁S₂ = S₂S₃ = S₃S₄ = S₄S₅ को मिला दें।
6. बिंदु H और S₃ को मिलाइए।
7. बिंदु S₅ से HS₃ को समांतर रेखा खींचिए। यह रेखा किरण SH को बिंदु V पर प्रतिच्छेदित करती है।
8. बिंदु V से भुजा HR को समांतर रेखा खींचें। इस रेखा और किरण SR के प्रतिच्छेदन बिंदु U का नाम दें।
   ΔSVU यह ΔSHR के समरूप अभीष्ट त्रिभुज है।