Advertisements
Advertisements
Question
सिद्ध कीजिए कि किसी बाह्य बिंदु से वृत्त पर खींची गई दो स्पर्श रेखाओं के बीच का कोण, केंद्र से संपर्क बिंदुओं को मिलाने वाले रेखाखंडों द्वारा अंतरित कोण का संपूरक होता है।
Solution
दिया है: PA और PB एक बिंदु P से O केंद्र वाले वृत्त पर खींची गई स्पर्श रेखा हैं। साथ ही, रेखा खंड OA और OB भी खींचे गए हैं।

सिद्ध करना: ∠APB + ∠AOB = 180°
उपपत्ति: हम जानते हैं कि वृत्त की स्पर्श रेखा संपर्क बिंदु से जाने वाली त्रिज्या पर लम्ब होती है।
अब, समकोण ΔOAP और समकोण ΔOBP में, हमारे पास PA = PB है...[बाहरी बिंदु से वृत्त की स्पर्श रेखाएँ]
OA = OB ...[एक ही वृत्त की त्रिज्या]
OP= OP ....[सामान्य]
ΔOAP ≅ ΔOBP
∠OPA = ∠OPB
और ∠AOP = ∠BOP
⇒∠APB = 2∠OPA तथा ∠AOB = 2∠AOP
दाईं ओर ΔOAP
⇒∠AOP + ∠OPA + ∠PAO = 180°
⇒∠AOP = 180° − 90° − ∠OPA
⇒∠AOP = 90° − ∠OPA
⇒2∠AOP = 180° − 2∠OPA
⇒∠AOB = 180° − ∠APB
⇒∠AOB + ∠APB = 180°
APPEARS IN
RELATED QUESTIONS
सिद्ध कीजिए कि किसी वृत्त के किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ समांतर होती हैं।
सिद्ध कीजिए कि स्पर्श बिन्दु से स्पर्श रेखा पर खींचा गया लम्ब वृत्त के केन्द्र से होकर जाता है।
एक बिन्दु A से, जो एक वृत्त के केन्द्र से 5 cm की दूरी पर है, वृत्त पर स्पर्श रेखा की लम्बाई 4 cm है। वृत्त की त्रिज्या ज्ञात कीजिए।
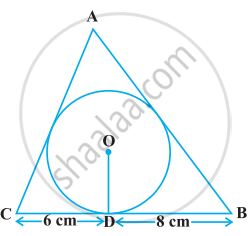
4 cm त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज ABC इस प्रकार खींचा गया है कि रेखाखंड BD और DC (जिनमें स्पर्श बिन्दु D द्वारा BC विभाजित है) की लम्बाईयाँ क्रमश: 8 cm और 6 cm हैं (देखिए आकृति)। भुजाएँ AB और AC ज्ञात कीजिए।
केंद्र O वाले वृत्त पर किसी बाहरी बिंदु P से खींची गई स्पर्श रेखा की लंबाई OP से सदैव छोटी होती है।
वृत्त की दो स्पर्श रेखाओं के बीच का कोण 0° हो सकता है।
सिद्ध कीजिए कि दो प्रतिच्छेदी रेखाओं को स्पर्श करने वाले वृत्त का केंद्र इन रेखाओं से बने कोण के समद्विभाजक पर स्थित होता है।
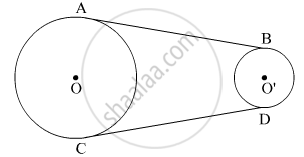
आकृति में, AB और CD असमान त्रिज्याओं वाले दो वृत्तों की उभयनिष्ठ स्पर्श रेखाएँ हैं। सिद्ध कीजिए कि AB = CD हैं।
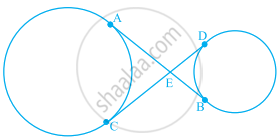
आकृति में, दोनों वृत्तों की उभयनिष्ठ स्पर्श रेखाएँ AB और CD परस्पर बिंदु E पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि AB = CD है।
केंद्र O और त्रिज्या 5 cm वाले एक वृत्त के केंद्र से 13 cm की दूरी पर एक बिंदु A है। AP और AQ क्रमश: बिंदुओं P और Q पर वृत्त की स्पर्श रेखाएँ हैं। यदि लघु चाप PQ पर स्थित एक बिंदु R पर एक स्पर्श रेखा BC ऐसी खींची जाए, जो AP को B और AQ को C पर प्रतिच्छेद करे, तो ΔABC का परिमाप ज्ञात कीजिए।
