Advertisements
Advertisements
Question
सिद्ध कीजिए कि R त्रिज्या के गोले के अन्तर्गत विशालतम शंकु का आयतन गोले के आयतन का `8/27` होता है।
Solution
माना VAB गोले के अन्तर्गत विशालतम शंकु का आयतन है।
स्पष्टतयाः अधिकतम आयतन के लिए शंकु का अक्ष गोले की ऊँचाई के साथ होना चाहिए।
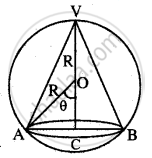
माना ∠AOC = θ
∴ AC, शंकु के आधार की त्रिज्या = R sin θ, जहाँ R
गोले की त्रिज्या है।
शंकु की ऊँचाई VC = VO + OC = R + R cos θ
शंकु का आयतन; V = `1/3 pi (AC)^2 xx (VC)`
`=> V = 1/3 piR^2 sin^2 θ (R + R cos theta)`
`=> V = 1/3 piR^3 sin^2 theta (1 + cos theta)`
अवकलन करने पर,
`therefore (dV)/(d theta) = 1/3 piR^3 [sin^2 theta (- sin theta) + (1 cos theta) * 2 sin theta cos theta]`
`= 1/3 piR^3 [- sin^3 theta + 2 sin theta cos theta + 2 sin theta (1 - sin^2 theta)]`
`= 1/3 piR^3 [- sin^3 theta + 2 sin theta cos theta + 2 sin theta - 2sin^2 theta]`
`= 1/3 pi R^3 [- 3 sin^3 theta + 2 sin theta + 2 sin theta cos theta]`
न्यूनतम व अधिकतम के लिए, `(dV)/(d theta) = 0`
`=> 1/3 piR^3 (- 3 sin^3 theta + 2 sin cos theta + 2 sin theta)` = 0
= - 3 sin3 θ + 2 sin θ cos θ + 2 sin θ = 0
= sin θ (- 3 sin2 θ + 2 cos θ + 2) = 0
= - 3 sin2 θ + 2 cos θ +2 = 0 ...[∵ sin θ ≠ 0]
= -3 (1 - cos2 θ) + 2 cos θ + 2 = 0
= - 3 + cos2 θ + 2 cos θ + 2 = 0
⇒ 3 cos2 θ + 2 cos θ - 1 = 0
⇒ (3 cos θ - 1)(cos θ + 1) = 0
⇒ cos θ = `1/3` cos θ = - 1
परन्तु cos θ ≠ 1 क्योंकि cos θ = - 1 ⇒ θ = π जो कि संभव नहीं है।
`therefore cos theta = 1/3`
जब `cos theta = 1/3`, तब `sin theta = sqrt(1 - cos^2 theta) = sqrt(1 - 1/9)`
`= sqrt(8/9)`
`= (2 sqrt2)/3`
अब `(dV)/(d theta) = 1/3 piR^3 sin theta [- 3 sin^2 theta + 2 + 2 cos theta]`
`= 1/3 piR^3 sin theta (3 cos theta - 1)(cos theta + 1)`
`cos theta = 1/3, dV/(d theta)` का चिन्ह + ve से -ve हो जाता है।
∴ V, `theta = cos^-1 (1/3)` पर उच्चतम है।
θ घटाने पर cos θ में वृद्धि होती है।
अब cos θ = `1/3` है तो V अधिकतम है।
cos θ के इस मान के लिए शंकु की ऊँचाई
VC = R + R cos θ
`= R + R xx 1/3 = (4R)/3`
शंकु की त्रिज्या = AC = R sin θ = `R * (2sqrt2)/3 = (2 sqrt2)/3 R`
∴ शंकु का अधिकतम आयतन V
`= 1/3 pi (AC)^2 (VC)`
`= 1/3 pi ((2 sqrt2 R)/3)^2 ((4R')/3)`
`= 1/3 pi xx 8/9 R^2 xx (4R)/3`
`= 8/27 (4/3 piR^3)`
`= 8/27 xx` गोले का आयतन
APPEARS IN
RELATED QUESTIONS
`y = [x (x - 1) + 1]^(1/3), 0 le x le 1,` का उच्चतम मान है:
अंतराल [1, 3] में 2x3 - 24x + 107 का महत्तम मान ज्ञात कीजिए। इसी फलन का अंतराल [-3, -1] में भी महत्तम मान ज्ञात कीजिए।
यदि लाभ फलन p(x) = 41 - 72x - 18x2 से प्रदत्त है तो किसी कंपनी द्वारा अर्जित उच्चतम लाभ ज्ञात कीजिए।
निम्नलिखित दिए गए फलन के उच्चतम या निम्नतम मान, यदि कोई हो तो ज्ञात कीजिए:
f(x) = (2x - 1)2 + 3
निम्नलिखित दिए गए फलन के उच्चतम या निम्नतम मान, यदि कोई हो तो ज्ञात कीजिए:
g(x) = x3 + 1
निम्नलिखित दिए गए फलन के उच्चतम मान या निम्नतम मान, यदि कोई हो तो, ज्ञात कीजिए:
f(x) = |x + 2| - 1
निम्नलिखित दिए गए फलन के उच्चतम मान या निम्नतम मान, यदि कोई हो तो, ज्ञात कीजिए:
g(x) = - |x + 1| + 3
निम्नलिखित दिए गए फलन के उच्चतम मान या निम्नतम मान, यदि कोई हो तो, ज्ञात कीजिए:
h(x) = sin (2x) + 5
निम्नलिखित दिए गए फलन के उच्चतम मान या निम्नतम मान, यदि कोई हो तो, ज्ञात कीजिए:
h(x) = x + 1, x ∈ (-1,1)
निम्नलिखित फलन के स्थानीय उच्चतम या निम्नतम, यदि कोई हो तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम माने, जैसी स्थिति हो, भी ज्ञात कीजिए।
f(x) = x2
निम्नलिखित फलन के स्थानीय उच्चतम या निम्नतम, यदि कोई हो तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम माने, जैसी स्थिति हो, भी ज्ञात कीजिए।
f(x) = x3 - 6x2 + 9x + 15
निम्नलिखित फलन के स्थानीय उच्चतम या निम्नतम, यदि कोई हो तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम माने, जैसी स्थिति हो, भी ज्ञात कीजिए।
g(x) = `x/2 + 2/x, x > 0`
निम्नलिखित फलन के स्थानीय उच्चतम या निम्नतम, यदि कोई हो तो ज्ञात कीजिए तथा स्थानीय उच्चतम या स्थानीय निम्नतम माने, जैसी स्थिति हो, भी ज्ञात कीजिए।
f(x) `= x sqrt(1 - x), 0 < x < 1`
सिद्ध कीजिए कि निम्नलिखित फलन को उच्चतम या निम्नतम मान नहीं है:
g(x) = log x
सिद्ध कीजिए कि निम्नलिखित फलन को उच्चतम या निम्नतम मान नहीं है:
h(x) = x3 + x2 + x + 1
प्रदत्त अंतराल में निम्नलिखित फलन के निरपेक्ष उच्चतम मान और निरपेक्ष निम्नतम मान ज्ञात कीजिए।
f(x) = x3, x ∈ [-2, 2]
प्रदत्त अंतराल में निम्नलिखित फलन के निरपेक्ष उच्चतम मान और निरपेक्ष निम्नतम मान ज्ञात कीजिए।
f(x) = sin x + cos x, x `in [0, pi]`
प्रदत्त अंतराल में निम्नलिखित फलन के निरपेक्ष उच्चतम मान और निरपेक्ष निम्नतम मान ज्ञात कीजिए।
f(x) = (x - 1)2 + 3, x `in` [-3, 1]
ऐसी दो संख्याएँ ज्ञात कीजिए जिनका योग 24 है और जिनका गुणनफल उच्चतम हो।
ऐसी दो धन संख्याएँ x और y ज्ञात कीजिए जिनका योग 35 हो और गुणनफल x2y5 उच्चतम हो।
सिद्ध कीजिए कि प्रदत्त पृष्ठ एवं महत्तम आयतन के बेलन की ऊँचाई आधार के व्यास के बराबर होती है।
सिद्ध कीजिए कि दी हुई तिर्यक ऊँचाई और महत्तम आयतन वाले शंकु का अर्थ शीर्ष कोण tan-1 `sqrt2` होता है।
सिद्ध कीजिए कि एक R त्रिज्या के गोले के अन्तर्गत अधिकतम आयतन के बेलन की ऊँचाई `(2R)/sqrt3` है। अधिकतम आयतन भी ज्ञात कीजिए।
सिद्ध कीजिए कि अर्द्धशीर्ष कोण और ऊँचाई h के लम्ब वृत्तीय शंकु के अन्तर्गत अधिकतम आयतन के बेलन की ऊँचाई शंकु के ऊँचाई की एक-तिहाई है और बेलन का अधिकतम आयतन `4/27` = πh3 tan2 α है।
वक्र x = t2 + 3t – 8, y = 2t2 – 2t -5 के बिन्दु (2, -1) पर स्पर्श रेखा की प्रवणता है-
