Advertisements
Advertisements
Question
Simplify the following using multiplication and division properties of surds:
`[sqrt(225/729) - sqrt(25/144)] ÷ sqrt(16/81)`
Solution
`[sqrt(225/729) - sqrt(25/144)] ÷ sqrt(16/81)`
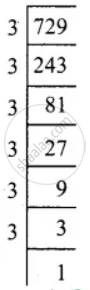
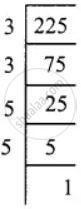
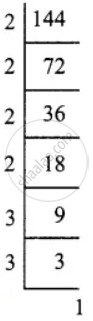

= `[ sqrt((3^2 xx 5^2)/(3^2 xx 3^2 xx 3^2)) - sqrt((5^2)/(2^2 xx 2^2 xx 3^2))] ÷ sqrt(2^4/3^4)`
= `[(3 xx 5)/(3 xx 3 xx 3) - 5/(2 xx 2 xx 3)] ÷ 2^2/3^2`
= `[5/9 - 5/12] ÷ 4/9`
= `((20 - 15)/36) ÷ 4/9`
= `5/36 xx 9/4`
= `(5 xx 1)/(4 xx 4)`
= `5/16`
APPEARS IN
RELATED QUESTIONS
Simplify.
`sqrt 7 - 3/5 sqrt 7 + 2 sqrt 7`
Multiply and write the answer in the simplest form.
`3 sqrt 12 xx sqrt 18`
Multiply and write the answer in the simplest form.
`5 sqrt 8 xx 2 sqrt 8`
Divide and write the answer in simplest form.
`sqrt98 ÷ sqrt 2`
Simplify.
`sqrt 216 - 5 sqrt 6 +sqrt 294 -3/sqrt6`
Simplify.
`4 sqrt 12 - sqrt 75 - 7 sqrt 48`
Simplify the following using multiplication and division properties of surds:
`sqrt(3) xx sqrt(5) xx sqrt(2)`
Simplify the following using multiplication and division properties of surds:
`root(3)(27) xx root(3)(8) xx root(3)(125)`
Simplify the following using multiplication and division properties of surds:
`(7sqrt("a") - 5sqrt("b")) (7sqrt("a") + 5sqrt("b"))`
`sqrt(27) + sqrt(12)` =
