Advertisements
Advertisements
Question
समचतुर्भुज की भुजाओं के वर्गों का योगफल उसके विकणों के वर्गों के योगफल के बराबर होता है, यह सिद्ध करने के लिए निम्नलिखित कृति पूर्ण कीजिए।
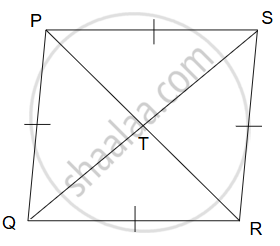
दत्त:
`square`PQRS एक समचतुर्भुज है जिसमें विकर्ण PR और विकर्ण SQ परस्पर बिंदु T पर प्रतिच्छेदित करते हैं।
साध्य: PS2 + SR2 + QR2 + PQ2 = PR2 + QS2
कृति:
समचतुर्भुज के विकर्ण परस्पर एक-दूसरे को समद्विभाजित करते हैं।
ΔPQS में, PT माध्यिका है तथा ΔQRS में, RT माध्यिका है।
∴ अपोलोनियस के प्रमेयानुसार,
PQ2 + PS2 = `square` + 2QT2 ...(I)
QR2 + SR2 = `square` + 2QT2 ...(II)
(I) तथा (II) को जोड़ने पर,
PQ2 + PS2 + QR2 + SR2 = 2(PT2 + `square`) + 4QT2
= 2(PT2 + `square`) + 4QT2 ...(RT = PT)
= 4PT2 + 4QT2
= (`square`)2 + (2QT)2
∴ PQ2 + PS2 + QR2 + SR2 = PR2 + `square`
Solution
दत्त:
`square`PQRS एक समचतुर्भुज है जिसमें विकर्ण PR और विकर्ण SQ परस्पर बिंदु T पर प्रतिच्छेदित करते हैं।
साध्य: PS2 + SR2 + QR2 + PQ2 = PR2 + QS2
कृति:
समचतुर्भुज के विकर्ण परस्पर एक-दूसरे को समद्विभाजित करते हैं।
ΔPQS में, PT माध्यिका है तथा ΔQRS में, RT माध्यिका है।
∴ अपोलोनियस के प्रमेयानुसार,
PQ2 + PS2 = \[\boxed{2\text{PT}^2}\] + 2QT2 ...(I)
QR2 + SR2 = \[\boxed{2\text{RT}^2}\] + 2QT2 ...(II)
(I) तथा (II) को जोड़ने पर,
PQ2 + PS2 + QR2 + SR2 = \[{2(\text{PT}^2 + \boxed{\text{RT}^2})}\] + 4QT2
= \[{2(\text{PT}^2 + \boxed{\text{PT}^2})}\] + 4QT2 ...(RT = PT)
= 4PT2 + 4QT2
= \[\boxed{(2\text{PT)}^2}\] + (2QT)2
∴ PQ2 + PS2 + QR2 + SR2 = PR2 + \[\boxed{\text{QS}^2}\]
