Advertisements
Advertisements
Question
समद्विभुज काटकोन त्रिकोणाची बाजू x आहे, तर त्याच्या कर्णाची लांबी काढा.
Solution
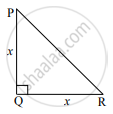
समजा, ΔPQR हा समद्विभुज काटकोन त्रिकोण आहे.
PQ = QR = x.
ΔPQR मध्ये, ∠Q = 90°
∴ PR2 = PQ2 + QR2 ....[पायथागोरसचे प्रमेय]
= x2 + x2
= 2x2
∴ PR = `sqrt(2x^2)` .....[दोन्ही बाजूंचे वर्गमूळ घेऊन]
= `xsqrt2` एकक
∴ समद्विभुज काटकोन त्रिकोणाच्या कर्णाची लांबी `xsqrt2` एकक आहे.
APPEARS IN
RELATED QUESTIONS
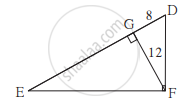
आकृती मध्ये ∠DFE = 90°, रेख FG ⊥ रेख ED. जर GD = 8, FG = 12, तर (1) EG (2) FD आणि (3) EF काढा.
रस्त्याच्या दुतर्फा असलेल्या इमारतीच्या भिंती एकमेकींना समांतर आहेत. 5.8 मी लांबीच्या शिडीचे एक टोक रस्त्यावर ठेवले असता तिचे वरचे टोक पहिल्या इमारतीच्या 4 मीटर उंच असलेल्या खिडकीपर्यंत टेकते. त्याच ठिकाणी शिडी ठेवून रस्त्याच्या दुसऱ्या बाजूस वळविल्यास तिचे वरचे टोक दुसऱ्या इमारतीच्या 4.2 मीटर उंच असलेल्या खिडकीपर्यंत येते, तर रस्त्याची रुंदी काढा.
आयताच्या बाजू 11 सेमी व 60 सेमी असतील, तर त्याच्या कर्णाची लांबी काढा.
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
एका आयताची एक बाजू 12 आणि कर्णाची लांबी 20 असेल, तर त्या आयताच्या दुसऱ्या बाजूची लांबी किती?
एका काटकोन त्रिकोणामध्ये काटकोन करणाऱ्या बाजू 24 सेमी व 18 सेमी असतील, तर त्याच्या कर्णाची लांबी काढा.
एका आयताच्या बाजू अनुक्रमे 35 मीटर आणि 12 मीटर असल्यास त्याचा कर्ण किती?
10 मीटर लांबीची एक शिडी जमिनीपासून 8 मीटर उंचीच्या एका खिडकीपाशी पोहोचते, तर त्या भिंतीचा पाया व शिडीचे खालचे टोक यांमधील अंतर काढण्यासाठी खालील कृती पूर्ण करा.
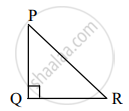
कृती: समजा, सोबतच्या आकृतीत,
PQ ही भिंतीची उंची आहे.
PR ही शिडी आहे आणि QR त्या भिंतीचा पाया व शिडीचे खालचे टोक यांमधील अंतर आहे.
∆PQR मध्ये, ∠PQR = 90°,
पायथागोरसच्या प्रमेयानुसार, PQ2 + `square` = PR2 … (i)
PR = 10, PQ = `square`
या किमती (i) मध्ये ठेवून,
QR2 + 82 = 102
QR2 = 102 – 82
QR2 = `square - 64`
QR2 = `square`
QR = 6
यावरून, त्या भिंतीचा पाया व शिडीचे खालचे टोक यांमधील अंतर 6 मीटर आहे.
∆LMN मध्ये, l = 5, m = 13, n = 12, तर ∆LMN हा काटकोन त्रिकोण आहे किंवा नाही ते ठरवण्यासाठी कृती करा. [l, m, n या ∠L, ∠M, व ∠N यांच्या समोरील बाजू आहेत.]
कृती: ∆LMN मध्ये, l = 5, m = 13, n = `square`
l2 = `square`, m2 = 169; n2 = 144.
l2 + n2 = 25 + 144 = `square`
`square^2` + l2 = m2
∴ पायथागोरसच्या प्रमेयानुसार, ∆LMN हा काटकोन त्रिकोण आहे.
समद्विभुज काटकोन त्रिकोणाच्या एकरूप बाजूंची लांबी 7 सेमी आहे. त्याची परिमिती काढा.
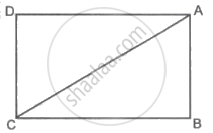
वरील आकृतीत `square`ABCD हा आयत आहे. जर AB = 5, AC = 13, तर बाजू BC ची लांबी काढण्यासाठी खालील कृती पर्ण करा.
कृती: ΔABC हा `square` त्रिकोण आहे.
∴ पायथागोरसच्या प्रमेयानुसार,
AB2 + BC2 = AC2
∴ 25 + BC2 = `square`
∴ BC2 = `square`
∴ BC = `square`
