Advertisements
Advertisements
Question
Solve the following quadratic equations by factorization:
(2x + 3)(3x − 7) = 0
Solution
We have,
(2x + 3)(3x − 7) = 0
⇒ (2x + 3) = 0 or (3x − 7) = 0
⇒ 2x = -3 or 3x = 7
⇒ x = -3/2 or x = 7/3
Thus, x = -3/2 and x = 7/3 are two roots of the equation (2x + 3)(3x − 7) = 0
APPEARS IN
RELATED QUESTIONS
Solve the following quadratic equations
(i) x2 + 5x = 0 (ii) x2 = 3x (iii) x2 = 4
Solve the following quadratic equations by factorization:
48x2 − 13x − 1 = 0
A pole has to be erected at a point on the boundary of a circular park of diameter 13 meters in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 meters. Is it the possible to do so? If yes, at what distances from the two gates should the pole be erected?
Solve the following quadratic equations by factorization:
`4(2x – 3)^2 – (2x – 3) – 14 = 0`
Write the set of value of 'a' for which the equation x2 + ax − 1 = 0 has real roots.
Solve equation using factorisation method:
`4/(x + 2) - 1/(x + 3) = 4/(2x + 1)`
Let ∆ ABC ∽ ∆ DEF and their areas be respectively, 64 cm2 and 121 cm2. If EF = 15⋅4 cm, find BC.
Solve the following equation by factorization
3x2= x + 4
Use the substitution y = 3x + 1 to solve for x : 5(3x + 1 )2 + 6(3x + 1) – 8 = 0
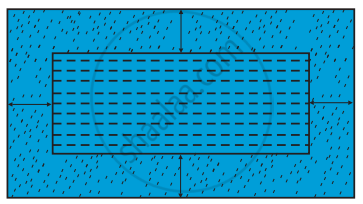
In the centre of a rectangular lawn of dimensions 50 m × 40 m, a rectangular pond has to be constructed so that the area of the grass surrounding the pond would be 1184 m2 [see figure]. Find the length and breadth of the pond.