Advertisements
Advertisements
Question
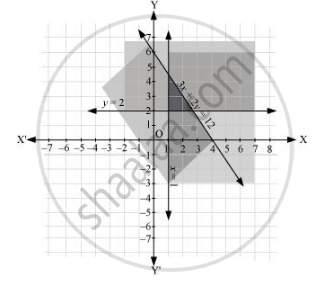
Solve the following system of inequalities graphically: 3x + 2y ≤ 12, x ≥ 1, y ≥ 2
Solution
3x + 2y ≤ 12 … (1)
x ≥ 1 … (2)
y ≥ 2 … (3)
The graphs of the lines, 3x + 2y = 12, x = 1, and y = 2, are drawn in the figure below.
Inequality (1) represents the region below the line, 3x + 2y = 12 (including the line 3x + 2y = 12). Inequality (2) represents the region on the right side of the line, x = 1 (including the line x = 1). Inequality (3) represents the region above the line, y = 2 (including the line y = 2).
Hence, the solution of the given system of linear inequalities is represented by the common shaded region including the points on the respective lines as follows.
APPEARS IN
RELATED QUESTIONS
Solve the following system of inequalities graphically: x ≥ 3, y ≥ 2
Solve the following system of inequalities graphically: 2x + y≥ 6, 3x + 4y ≤ 12
Solve the following system of inequalities graphically: x + y ≤ 6, x + y ≥ 4
Solve the following system of inequalities graphically: x + y ≤ 9, y > x, x ≥ 0
Solve the following system of inequalities graphically: 3x + 4y ≤ 60, x + 3y ≤ 30, x ≥ 0, y ≥ 0
Solve the following system of inequalities graphically: 2x + y≥ 4, x + y ≤ 3, 2x – 3y ≤ 6
Solve the following system of inequalities graphically: x – 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1
Solve the following system of inequalities graphically: 4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, x, y ≥ 0
Solve the following system of inequalities graphically: 3x + 2y ≤ 150, x + 4y ≤ 80, x ≤ 15, y ≥ 0, x ≥ 0
Solve the following system of inequalities graphically: x + 2y ≤ 10, x + y ≥ 1, x – y ≤ 0, x ≥ 0, y ≥ 0
Find all pairs of consecutive odd positive integers, both of which are smaller than 10, such that their sum is more than 11.
Find all pairs of consecutive odd natural number, both of which are larger than 10, such that their sum is less than 40.
The marks scored by Rohit in two tests were 65 and 70. Find the minimum marks he should score in the third test to have an average of at least 65 marks.
A company manufactures cassettes and its cost and revenue functions for a week are \[C = 300 + \frac{3}{2}x \text{ and } R = 2x\] respectively, where x is the number of cassettes produced and sold in a week. How many cassettes must be sold for the company to realize a profit?
The longest side of a triangle is three times the shortest side and third side is 2 cm shorter than the longest side if the perimeter of the triangles at least 61 cm, find the minimum length of the shortest-side.
How many litres of water will have to be added to 1125 litres of the 45% solution of acid so that the resulting mixture will contain more than 25% but less than 30% acid content?
Write the set of values of x satisfying the inequation (x2 − 2x + 1) (x − 4) < 0.
Write the solution set of the inequation \[\left| \frac{1}{x} - 2 \right| > 4\]
Write the number of integral solutions of \[\frac{x + 2}{x^2 + 1} > \frac{1}{2}\]
Write the solution of set of\[\left| x + \frac{1}{x} \right| > 2\]
Write the solution set of the inequation |x − 1| ≥ |x − 3|.
Solve the following system of inequalities `(2x + 1)/(7x - 1) > 5, (x + 7)/(x - 8) > 2`
Show that the following system of linear inequalities has no solution x + 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1
Solve the following system of linear inequalities:
3x + 2y ≥ 24, 3x + y ≤ 15, x ≥ 4
Show that the solution set of the following system of linear inequalities is an unbounded region 2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0.
Solution set of x ≥ 0 and y ≤ 0 is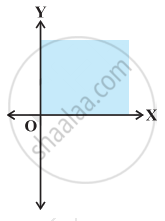
Solution set of x ≥ 0 and y ≤ 1 is