Advertisements
Advertisements
Question
Solve the following system of inequalities `(2x + 1)/(7x - 1) > 5, (x + 7)/(x - 8) > 2`
Solution
`(2x + 1)/(7x - 1) > 5`
Subtracting 5 both side, we get
`(2x + 1)/(7x - 1) - 5 > 0`
⇒ `(2x + 1- 35x + 5)/(7x - 1) > 0`
⇒ `(6 - 33x)/(7x - 1) > 0`
For above fraction be greater than 0, either both denominator and numerator should be greater than 0 or both should be less than 0.
⇒ 6 – 33x > 0 and 7x – 1 > 0
⇒ 33x < 6 and 7x > 1
⇒ x < `2/11` and x > `1/7`
⇒ `1/7` < x < `2/11` ......(i)
Or
⇒ 6 – 33x < 0 and 7x – 1 < 0
⇒ 33x > 6 and 7x < 1
⇒ x > `2/11` and x < `1/7`
⇒ `2/11< x < 1/7` ......(Which is not possible since `1/7 > 2/11`)
Also, `(x + 7)/(x - 8) > 2`
Subtracting 2 both sides, we get
⇒ `(x + 7)/(x - 8) - 2 > 0`
⇒ `(x + 7 - 2x + 16)/(x - 8) > 0`
⇒ `(23 - x)/(x - 8) > 0`
For above fraction be greater than 0.
Either both denominator and numerator should be greater than 0 or both should be less than 0.
⇒ 23 – x > 0 and x – 8 > 0
⇒ x < 23 and x > 8
⇒ 8 < x < 23 ......(ii)
Or
23 – x < 0 and x – 8 < 0
⇒ x > 23 and x < 8
⇒ 23 < x < 8 ......(Which is not possible, as 23 > 8]
Therefore, from equations (i) and (ii).
We infer that there is no solution satisfying both inequalities.
Hence, the given system has no solution.
APPEARS IN
RELATED QUESTIONS
Solve the following system of inequalities graphically: x + y≥ 4, 2x – y > 0
Solve the following system of inequalities graphically: 2x + y≥ 8, x + 2y ≥ 10
Solve the following system of inequalities graphically: 5x + 4y ≤ 20, x ≥ 1, y ≥ 2
Solve the following system of inequalities graphically: 2x + y≥ 4, x + y ≤ 3, 2x – 3y ≤ 6
Solve the following system of inequalities graphically: 4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, x, y ≥ 0
Find all pairs of consecutive odd positive integers, both of which are smaller than 10, such that their sum is more than 11.
Find all pairs of consecutive even positive integers, both of which are larger than 5, such that their sum is less than 23.
A solution is to be kept between 30°C and 35°C. What is the range of temperature in degree Fahrenheit?
How many litres of water will have to be added to 1125 litres of the 45% solution of acid so that the resulting mixture will contain more than 25% but less than 30% acid content?
The water acidity in a pool is considered normal when the average pH reading of three daily measurements is between 7.2 and 7.8. If the first two pH reading are 7.48 and 7.85, find the range of pH value for the third reading that will result in the acidity level being normal.
Write the solution set of the equation |2 − x| = x − 2.
Write the solution set of the inequation \[\left| \frac{1}{x} - 2 \right| > 4\]
Write the number of integral solutions of \[\frac{x + 2}{x^2 + 1} > \frac{1}{2}\]
Write the set of values of x satisfying the inequations 5x + 2 < 3x + 8 and \[\frac{x + 2}{x - 1} < 4\]
Write the solution of set of\[\left| x + \frac{1}{x} \right| > 2\]
Write the solution set of the inequation |x − 1| ≥ |x − 3|.
Solve each of the following system of equations in R.
\[5x - 7 < 3\left( x + 3 \right), 1 - \frac{3x}{2} \geq x - 4\]
Find the graphical solution of the following system of linear inequations:
x – y ≤ 0, 2x – y ≥ − 2
Find the graphical solution of the following system of linear inequations:
3x + 2y ≤ 1800, 2x + 7y ≤ 1400
Solve the following system of inequalities graphically.
2x – y ≥ 1, x – 2y ≤ – 1
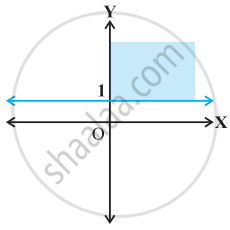
Find the linear inequalities for which the shaded region in the given figure is the solution set.
Find the linear inequalities for which the shaded region in the given figure is the solution set.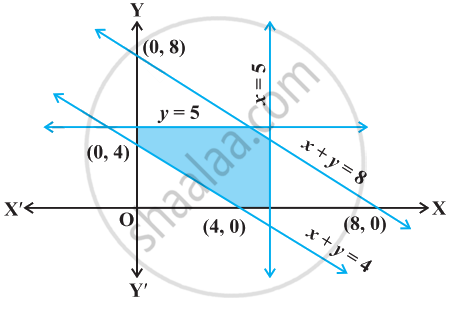
Solution set of x ≥ 0 and y ≤ 1 is