Advertisements
Advertisements
Question
Find the graphical solution of the following system of linear inequations:
3x + 2y ≤ 1800, 2x + 7y ≤ 1400
Solution
To find a graphical solution, construct the table as follows:
| Inequation | Inequation | Double Intercept form | Points (x, y) | Region |
| 3x + 2y ≤ 1800 | 3x + 2y = 1800 | `"x"/600+"y"/900=1` | A (600, 0), B (0, 900) |
3(0) + 2(0) ≤ 1800 ∴ 0 ≤ 1800 ∴ origin side |
| 2x + 7y ≤ 1400 | 2x + 7y = 1400 | `"x"/700+"y"/200=1` | C (700, 0), D (0, 200) |
2(0) + 7(0) ≤ 1400 ∴ 0 ≤ 1400 ∴ origin side |
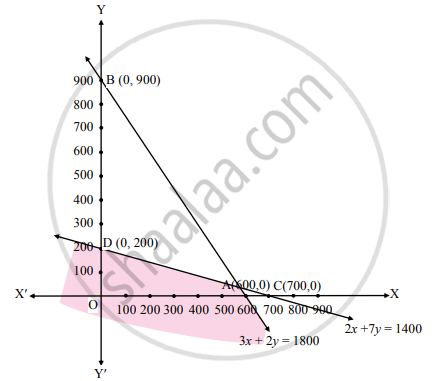
Shaded portion represents the graphical solution.
APPEARS IN
RELATED QUESTIONS
Solve the following system of inequalities graphically: x ≥ 3, y ≥ 2
Solve the following system of inequalities graphically: 3x + 2y ≤ 12, x ≥ 1, y ≥ 2
Solve the following system of inequalities graphically: x + y ≤ 9, y > x, x ≥ 0
Solve the following system of inequalities graphically: 5x + 4y ≤ 20, x ≥ 1, y ≥ 2
Solve the following system of inequalities graphically: 3x + 4y ≤ 60, x + 3y ≤ 30, x ≥ 0, y ≥ 0
Solve the following system of inequalities graphically: x – 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1
Solve the following system of inequalities graphically: 4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, x, y ≥ 0
The marks scored by Rohit in two tests were 65 and 70. Find the minimum marks he should score in the third test to have an average of at least 65 marks.
A solution is to be kept between 86° and 95°F. What is the range of temperature in degree Celsius, if the Celsius (C)/ Fahrenheit (F) conversion formula is given by\[F = \frac{9}{5}C + 32\]
A company manufactures cassettes and its cost and revenue functions for a week are \[C = 300 + \frac{3}{2}x \text{ and } R = 2x\] respectively, where x is the number of cassettes produced and sold in a week. How many cassettes must be sold for the company to realize a profit?
A solution of 8% boric acid is to be diluted by adding a 2% boric acid solution to it. The resulting mixture is to be more than 4% but less than 6% boric acid. If there are 640 litres of the 8% solution, how many litres of 2% solution will have to be added?
Write the solution set of the inequation \[\left| \frac{1}{x} - 2 \right| > 4\]
Find the graphical solution of the following system of linear inequations:
x – y ≤ 0, 2x – y ≥ − 2
Find the graphical solution of the following system of linear inequations:
2x + 3y ≥ 12, – x + y ≤ 3, x ≤ 4, y ≥ 3
Find the linear inequalities for which the shaded region in the given figure is the solution set.
Find the linear inequalities for which the shaded region in the given figure is the solution set.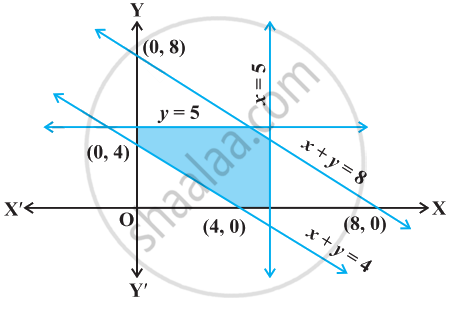
Show that the solution set of the following system of linear inequalities is an unbounded region 2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0.
Solution set of x ≥ 0 and y ≤ 1 is