Advertisements
Advertisements
Question
Solve the following system of inequalities graphically: 2x + y≥ 4, x + y ≤ 3, 2x – 3y ≤ 6
Solution
2x + y≥ 4 … (1)
x + y ≤ 3 … (2)
2x – 3y ≤ 6 … (3)
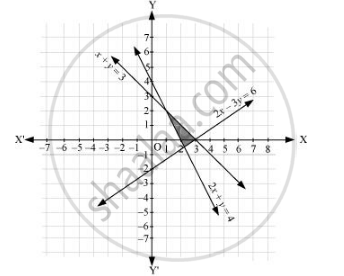
The graph of the lines, 2x + y= 4, x + y = 3, and 2x – 3y = 6, are drawn in the figure below.
Inequality (1) represents the region above the line, 2x + y= 4 (including the line 2x + y= 4). Inequality (2) represents the region below the line,
x + y = 3 (including the line x + y = 3). Inequality (3) represents the region above the line, 2x – 3y = 6 (including the line 2x – 3y = 6).
Hence, the solution of the given system of linear inequalities is represented by the common shaded region including the points on the respective lines as follows.
APPEARS IN
RELATED QUESTIONS
Solve the following system of inequalities graphically: x ≥ 3, y ≥ 2
Solve the following system of inequalities graphically: 2x + y≥ 6, 3x + 4y ≤ 12
Solve the following system of inequalities graphically: x + y ≤ 6, x + y ≥ 4
Solve the following system of inequalities graphically: x + y ≤ 9, y > x, x ≥ 0
Solve the following system of inequalities graphically: 5x + 4y ≤ 20, x ≥ 1, y ≥ 2
Solve the following system of inequalities graphically: 3x + 4y ≤ 60, x + 3y ≤ 30, x ≥ 0, y ≥ 0
Solve the following system of inequalities graphically: x + 2y ≤ 10, x + y ≥ 1, x – y ≤ 0, x ≥ 0, y ≥ 0
Find all pairs of consecutive odd natural number, both of which are larger than 10, such that their sum is less than 40.
Find all pairs of consecutive even positive integers, both of which are larger than 5, such that their sum is less than 23.
The marks scored by Rohit in two tests were 65 and 70. Find the minimum marks he should score in the third test to have an average of at least 65 marks.
How many litres of water will have to be added to 1125 litres of the 45% solution of acid so that the resulting mixture will contain more than 25% but less than 30% acid content?
Write the set of values of x satisfying the inequation (x2 − 2x + 1) (x − 4) < 0.
Write the solution set of the equation |2 − x| = x − 2.
Write the set of values of x satisfying |x − 1| ≤ 3 and |x − 1| ≥ 1.
Write the number of integral solutions of \[\frac{x + 2}{x^2 + 1} > \frac{1}{2}\]
Write the set of values of x satisfying the inequations 5x + 2 < 3x + 8 and \[\frac{x + 2}{x - 1} < 4\]
Write the solution set of the inequation |x − 1| ≥ |x − 3|.
Solve each of the following system of equations in R.
\[5x - 7 < 3\left( x + 3 \right), 1 - \frac{3x}{2} \geq x - 4\]
Find the graphical solution of the following system of linear inequations:
2x + 3y ≥ 12, – x + y ≤ 3, x ≤ 4, y ≥ 3
Solve the following system of inequalities graphically.
3x + 2y ≤ 12, x ≥ 1, y ≥ 2
Solve the following system of inequalities graphically.
2x – y ≥ 1, x – 2y ≤ – 1
Find the linear inequalities for which the shaded region in the given figure is the solution set.
Find the linear inequalities for which the shaded region in the given figure is the solution set.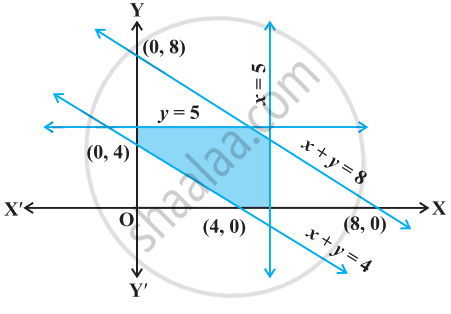
Show that the following system of linear inequalities has no solution x + 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1
Solve the following system of linear inequalities:
3x + 2y ≥ 24, 3x + y ≤ 15, x ≥ 4
Show that the solution set of the following system of linear inequalities is an unbounded region 2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0.
Solution set of x ≥ 0 and y ≤ 0 is
Solution set of x ≥ 0 and y ≤ 1 is