Advertisements
Advertisements
Question
Solve the following inequalities and represent the solution graphically on number line:
3x – 7 > 2(x – 6), 6 – x > 11 – 2x
Solution
3x – 7 > 2(x – 6)
⇒ 3x – 7 > 2x – 12
⇒ 3x – 2x > – 12 + 7
⇒ x > –5 …(1)
6 – x > 11 – 2x
⇒ –x + 2x > 11 – 6
⇒ x > 5 …(2)
From (1) and (2), it can be concluded that the solution set for the given system of inequalities is `(5, ∞)`. The solution of the given system of inequalities can be represented on number line as

APPEARS IN
RELATED QUESTIONS
Solve the given inequality graphically in two-dimensional plane: 3x + 4y ≤ 12
Solve the given inequality graphically in two-dimensional plane: x – y ≤ 2
Solve the given inequality graphically in two-dimensional plane: 2x – 3y > 6
Solve the given inequality graphically in two-dimensional plane: 3y – 5x < 30
Solve the given inequality graphically in two-dimensional plane: y < –2
Solve the inequalities and represent the solution graphically on number line:
5x + 1 > –24, 5x – 1 < 24
Solve the inequality and represent the solution graphically on number line:
2(x – 1) < x + 5, 3(x + 2) > 2 – x
Solve the inequalities and represent the solution graphically on number line:
5(2x – 7) – 3(2x + 3) ≤ 0, 2x + 19 ≤ 6x + 47
A solution of 8% boric acid is to be diluted by adding a 2% boric acid solution to it. The resulting mixture is to be more than 4% but less than 6% boric acid. If we have 640 litres of the 8% solution, how many litres of the 2% solution will have to be added?
IQ of a person is given by the formula
IQ = `(MA)/(CA) xx100`
Where MA is mental age and CA is chronological age. If 80 ≤ IQ ≤ 140 for a group of 12 years old children, find the range of their mental age.
Solve the following systems of linear inequation graphically:
2x + 3y ≤ 6, x + 4y ≤ 4, x ≥ 0, y ≥ 0
Solve the following systems of linear inequations graphically:
x − y ≤ 1, x + 2y ≤ 8, 2x + y ≥ 2, x ≥ 0, y ≥ 0
Solve the following systems of linear inequations graphically:
x + y ≥ 1, 7x + 9y ≤ 63, x ≤ 6, y ≤ 5, x ≥ 0, y ≥ 0
Show that the solution set of the following linear inequations is empty set:
x + 2y ≤ 3, 3x + 4y ≥ 12, y ≥ 1, x ≥ 0, y ≥ 0
Solve the following systems of inequations graphically:
2x + y ≥ 8, x + 2y ≥ 8, x + y ≤ 6
Solve the following systems of inequations graphically:
x + 2y ≤ 40, 3x + y ≥ 30, 4x + 3y ≥ 60, x ≥ 0, y ≥ 0
Solve the following systems of inequations graphically:
5x + y ≥ 10, 2x + 2y ≥ 12, x + 4y ≥ 12, x ≥ 0, y ≥ 0
Show that the following system of linear equations has no solution:
\[x + 2y \leq 3, 3x + 4y \geq 12, x \geq 0, y \geq 1\]
Mark the correct alternative in each of the following:
If x\[<\]7, then
Write the solution of the inequation\[\frac{x^2}{x - 2} > 0\]
Find the linear inequalities for which the shaded region in the given figure is the solution set.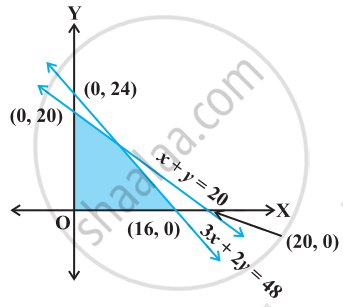
State which of the following statement is True or False.
If x < y and b < 0, then `x/"b" < y/"b"`
State which of the following statement is True or False.
If xy > 0, then x > 0 and y < 0
State which of the following statement is True or False.
If xy > 0, then x < 0 and y < 0
Graph of x ≥ 0 is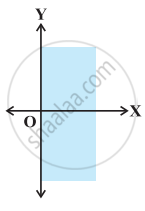
Solution set of x + y ≥ 0 is