Advertisements
Advertisements
Question
Solve the inequalities and represent the solution graphically on number line:
5x + 1 > –24, 5x – 1 < 24
Solution
5x + 1 > –24
⇒ 5x > –25
⇒ x > –5 … (1)
5x – 1 < 24
⇒ 5x < 25
⇒ x < 5 … (2)
From (1) and (2), it can be concluded that the solution set for the given system of inequalities is (–5, 5). The solution of the given system of inequalities can be represented on number line as

APPEARS IN
RELATED QUESTIONS
Solve the given inequality graphically in two-dimensional plane: x + y < 5
Solve the given inequality graphically in two-dimensional plane: 2x + y ≥ 6
Solve the given inequality graphically in two-dimensional plane: 3x + 4y ≤ 12
Solve the given inequality graphically in two-dimensional plane: y + 8 ≥ 2x
Solve the given inequality graphically in two-dimensional plane: x – y ≤ 2
Solve the given inequality graphically in two-dimensional plane: 2x – 3y > 6
Solve the given inequality graphically in two-dimensional plane: –3x + 2y ≥ –6
Solve the given inequality graphically in two-dimensional plane: 3y – 5x < 30
Solve the given inequality graphically in two-dimensional plane: y < –2
Solve the given inequality graphically in two-dimensional plane: x > –3
Solve the inequality and represent the solution graphically on number line:
2(x – 1) < x + 5, 3(x + 2) > 2 – x
Solve the following inequalities and represent the solution graphically on number line:
3x – 7 > 2(x – 6), 6 – x > 11 – 2x
IQ of a person is given by the formula
IQ = `(MA)/(CA) xx100`
Where MA is mental age and CA is chronological age. If 80 ≤ IQ ≤ 140 for a group of 12 years old children, find the range of their mental age.
Solve the following systems of linear inequation graphically:
2x + 3y ≤ 6, x + 4y ≤ 4, x ≥ 0, y ≥ 0
Solve the following systems of linear inequations graphically:
x − y ≤ 1, x + 2y ≤ 8, 2x + y ≥ 2, x ≥ 0, y ≥ 0
Solve the following systems of linear inequations graphically:
2x + 3y ≤ 35, y ≥ 3, x ≥ 2, x ≥ 0, y ≥ 0
Show that the solution set of the following linear inequations is empty set:
x − 2y ≥ 0, 2x − y ≤ −2, x ≥ 0, y ≥ 0
Show that the solution set of the following linear inequations is empty set:
x + 2y ≤ 3, 3x + 4y ≥ 12, y ≥ 1, x ≥ 0, y ≥ 0
Find the linear inequations for which the solution set is the shaded region given in Fig. 15.42
Show that the solution set of the following linear in equations is an unbounded set:
x + y ≥ 9
3x + y ≥ 12
x ≥ 0, y ≥ 0
Solve the following systems of inequations graphically:
12x + 12y ≤ 840, 3x + 6y ≤ 300, 8x + 4y ≤ 480, x ≥ 0, y ≥ 0
Solve the following systems of inequations graphically:
5x + y ≥ 10, 2x + 2y ≥ 12, x + 4y ≥ 12, x ≥ 0, y ≥ 0
Show that the following system of linear equations has no solution:
\[x + 2y \leq 3, 3x + 4y \geq 12, x \geq 0, y \geq 1\]
Show that the solution set of the following system of linear inequalities is an unbounded region:
\[2x + y \geq 8, x + 2y \geq 10, x \geq 0, y \geq 0\]
Write the solution of the inequation\[\frac{x^2}{x - 2} > 0\]
Find the linear inequalities for which the shaded region in the given figure is the solution set.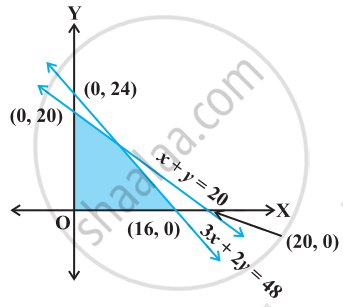
State which of the following statement is True or False.
If x < y and b < 0, then `x/"b" < y/"b"`
Solution set of x + y ≥ 0 is