Advertisements
Advertisements
Question
State whether the given algebraic expression are polynomial? Justify.
`2 - 5 sqrt x`
Solution
In an algebraic expression, if the powers of the variables are whole numbers then the algebraic expression is a polynomial.
`2 - 5 sqrt x = 2 - 5x^(1/2)`
Here, the power of x is `1/2`, which is not a whole number.
So, `2 - 5 sqrt x` is not a polynomial.
APPEARS IN
RELATED QUESTIONS
Classify the following polynomials as linear, quadratic, cubic and biquadratic polynomials:
`3y`
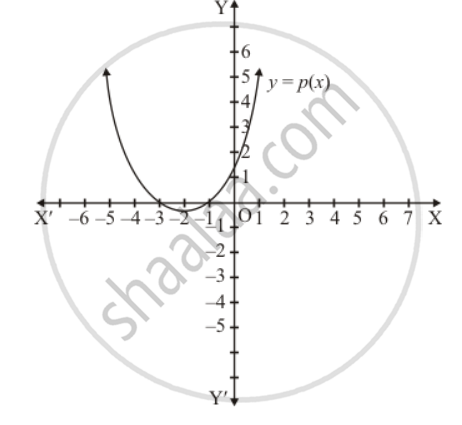
In Fig. 2.17, the graph of a polynomial p(x) is given. Find the zeros of the polynomial.
Write a quadratic polynomial, sum of whose zeros is \[2\sqrt{3}\] and their product is 2.
If one root of the polynomial f(x) = 5x2 + 13x + k is reciprocal of the other, then the value of k is
Divide. Write the quotient and the remainder.
(8p3 − 4p2) ÷ 2p2
Divide. Write the quotient and the remainder.
(6x5 − 4x4 + 8x3 + 2x2) ÷ 2x2
Obtain all the zeroes of the polynomial 2x4 − 5x3 − 11x2 + 20x + 12 when 2 and − 2 are two zeroes of the above polynomial.
Identify the following expression is polynomial. If not give reason:
`1/(x^(-2)) + 1/(x^(-1)) + 7`
The below picture are few natural examples of parabolic shape which is represented by a quadratic polynomial. A parabolic arch is an arch in the shape of a parabola. In structures, their curve represents an efficient method of load, and so can be found in bridges and in architecture in a variety of forms.




If α and `1/α` are the zeroes of the quadratic 2x2 − x + 8k, polynomial 2 then k is:
Classify the following as a constant, linear, quadratic and cubic polynomials:
2 – x2 + x3
