Advertisements
Advertisements
Question
Study the following circuit:
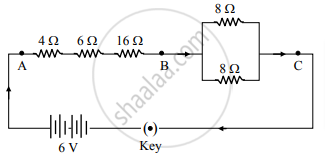
On the basis of this circuit, answer the following questions:
i. Find the value of total resistance between the points A and B.
ii. Find the resistance between the points B and C.
iii. Calculate the current drawn from the battery, when the key is closed
OR
iii. In the above circuit, the 16Ω resistor or the parallel combination of two resistors of 8 Ω, which one of the two will have more potential difference across its two ends? Justify your answer.
Solution
i. To find the total resistance between points A and B, we simply add up the resistances in series:
RAB = R4Ω + R6Ω + R16Ω = 4Ω + 6Ω + 16Ω = 26Ω
ii. The resistance between points B and C is a bit more complex because we have two resistances in parallel. We use the formula for resistances in parallel:
`1/R_(BC)=1/R_(8Ω,upper)+1/R_(8Ω,lower)`
`1/R_(BC)=1/(8Ω)+1/(8Ω)= 1/(4Ω)`
`R_(BC) = 4Ω`
iii. To calculate the current drawn from the battery when the key is closed, we need to find the total resistance in the circuit. The total resistance will be the sum of the resistance between A and B and the equivalent resistance between B and C which we found to be
RAB + RBC = 26Ω + 4Ω = 30Ω
Now, using Ohm's Law (V=IR), where V is the voltage of the battery, I is the current, and R is the total resistance, we can find the current:
`I = V/R = (6V)/(30Ω) = 0.2 A`
So, the current drawn from the battery is 0.2 A (or 200 mA).
OR
iii. The potential difference across a resistor in a circuit is given by Ohm's Law, which states:
V = I.R
where V is the potential difference, I is the current, and R is the resistance.
In the given circuit, the 16Ω resistor is in series with two other resistors (4Ω and 6Ω), and the combination of two 8Ω resistors is in parallel. The total resistance in series (4Ω + 6Ω + 16Ω = 26Ω) is greater than the effective resistance of the parallel combination of two 8Ω resistors which is 4Ω, since resistors in parallel have an effective resistance Rparallel given by
`1/R_("parallel")=1/R_1+1/R_2`
Therefore, the series combination (including the 16Ω resistor) has more resistance than the parallel combination, which means it will have more potential difference across it. Since the same current flows through the series resistors, the potential difference across the 16Ω resistor will be the largest among the individual resistors because it has the highest resistance.
So, the 16Ω resistor will have more potential difference across its ends than the parallel combination of two 8Ω resistors.
APPEARS IN
RELATED QUESTIONS
Complete the following :-
(b)

Show how you would connect three resistors, each of resistance 6 Ω, so that the combination has a resistance of 9 Ω.
In the circuit given below:
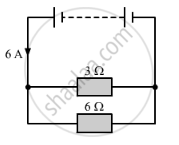
(a) What is the combined resistance?
(b) What is the p.d. across the combined resistor?
(c) What is the p.d. across the 3 Ω resistor?
(d) What is the current in the 3 Ω resistor?
(e) What is the current in the 6 Ω resistor?
In parallel combination of resistances ______.
Two resistors having resistance 4𝛀 and 6𝛀 are connected in parallel. Find their equivalent resistance.
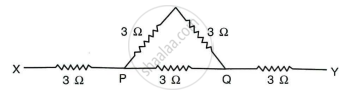
Five resistors, each 3 Ω, are connected as shown in Fig. Calculate the resistance
- between the points P and Q.
- between the points X and Y.
A uniform wire with a resistance of 27 Ω is divided into three equal pieces and then they are joined in parallel. Find the equivalent resistance of the parallel combination.
Calculate equivalent resistance in the following cases:
Two resistors when connected in parallel give the resultant resistance of 2 ohms, but when connected in series the effective resistance becomes 9 ohms. Calculate the value of each resistance.
