Advertisements
Advertisements
Question
Taking the volume of hydrogen as calculated in Q.19, what change must be made in Kelvin (absolute) temperature to return the volume to 2500 cm3 (pressure remaining constant)?
Solution
V1 = 714.29 cm3
P1 = P2 = P
T1 = 273 K
V2 = 2500 cm3
T2= ?
By using Charles's Law,
`("P"_1 "V"_1)/"T"_1 = ("PV"_2)/"T"_2`
Since P is constant, it cancels out.
`"V"_1/"T"_1 = "V"_2/"T"_2`
T2 = `("V"_2 xx "T"_1)/"V"_1`
T2 = `(2500 xx 273)/714.29`
T2 = 3.5 × 273
T2 = 955.5 K
∴ T2 = 3.5 times
∴ The temperature must be increased 3.5 times.
APPEARS IN
RELATED QUESTIONS
Explain Charles's law on the basis of the kinetic theory of matter.
State the law which is represented by the following graph:
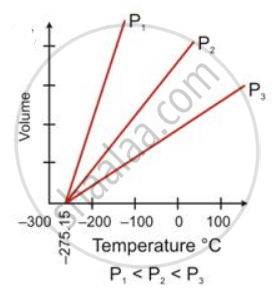
Give reasons for the following:
Mountaineers carry oxygen cylinders with them.
How did Charles's law lead to the concept of an absolute scale of temperature?
State the following:
Ice point in absolute temperature
Choose the correct answer:
The volume-temperature relationship is given by
What will be the minimum pressure required to compress 500 dm3 of air at 1 bar to 200 dm3 temperature remaining constant?
Give its
(i) graphical representation,
(ii) mathematical expression
(iii) significance
A certain mass of gas occupied 850 ml at a pressure of 760 mm of Hg. On increasing the pressure it was found that the volume of the gas was 75% of its initial value. Assuming constant temperature, find the final pressure of the gas?
The pressure on one mole of gas at s.t.p. is doubled and the temperature is raised to 546 K. What is the final volume of the gas ? [one mole of a gas occupies a volume of 22.4 litres at stp.]
