Advertisements
Advertisements
Question
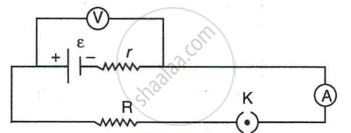
The diagram in Figure shows a cell of e.m.f. ε = 4 volt and internal resistance r = 2 ohm connected to an external resistance R = 8 ohm. The ammeter A measures the current in the circuit and the voltmeter V measures the terminal voltage across the cell. What will be the readings of the ammeter and voltmeter when
- the key K is open, and
- the key K is closed
Solution
ε = 4 volt
r = 2 ohm
R = 8 Ω
V = ?
I = ?
- When key is open: Since there will be no current flowing through the circuit, the voltmeter reads zero (A = 0) and the electromotive force (e.m.f.) of the cell is two volts.
- When key is closed:
`I = ε/("R" + r)`
= `(4 " volt")/(8 + 2)`
= `4/10`
= 0.4 A
Ammeter reading = 0.4 A
`"R" = "V"/"I"` or V = IR
V = 0.4 × 8
= 3.2 volt
voltmeter reading = 3.2 volt
RELATED QUESTIONS
A cell is used to send current to an external circuit.
- How does the voltage across its terminals compare with its e.m.f.?
- Under what condition is the e.m.f. of a cell equal to its terminal voltage?
A cell of e.m.f. 1.8V and internal resistance 2Ω is connected in series with an ammeter of resistance 0.7Ω and a resistor of 4.5Ω as shown in Fig.
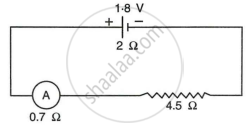
- What would be the reading of the ammeter?
- What is the potential difference across the terminals of the cell?
A battery of e.m.f. 15 V and internal resistance 3 ohm is connected to two resistors of resistances 3 ohm and 6 ohm is series Find:
(a) the current through the battery
(b) the p.d. between the terminals of the battery.
A cell of e.m.f. 2 V and internal resistance 1.2 Ω is connected to an ammeter of resistance 0.8 Ω and two resistors of 4.5 Ω and 9 Ω as shown in following figure.

Find:
- The reading of the ammeter,
- The potential difference across the terminals of the cells, and
- The potential difference across the 4.5 Ω resistor.
Four cells each of e.m.f. 2V and internal resistance 0.1 Ω are connected in series to an ammeter of negligible resistance, a 1.6 Ω resistor and an unknown resistor R1. The current in the circuit is 2A. Draw a labelled diagram and calculate:
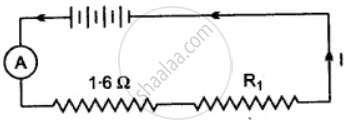
(i) Total resistance of the circuit,
(ii) Total e.m.f.
(iii) The value of R1 and
(iv) The p.d. across R1.
A cell supplies a current of 0.6 A through a 2Ω coil and a current of 0.3 A through on 8Ω coil. Calculate the e.m.f and internal resistance of the cell.
When a resistance of 3Ω is connected across a cell, the current flowing is 0.5 A. On changing the resistance to 7Ω, the current becomes 0.25A. Calculate the e.m.f. and the internal resistance of the cell.
Study the diagram:
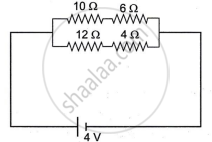
- Calculate the total resistance of the circuit.
- Calculate the current drawn from the cell.
- State whether the current through 10 Ω resistor is greater than, less than or equal to the current through the 12 Ω resistor.
Explain the meaning of the term internal resistance of a cell.
A battery of e.m.f. 6·0 V supplies current through a circuit in which the resistance can be changed. A high resistance voltmeter is connected across the battery. When the current is 3 A, the voltmeter reads 5.4 V. Find the internal resistance of the battery.
