Advertisements
Advertisements
Question
- The earth-moon distance is about 60 earth radius. What will be the diameter of the earth (approximately in degrees) as seen from the moon?
- Moon is seen to be of (½)°diameter from the earth. What must be the relative size compared to the earth?
- From parallax measurement, the sun is found to be at a distance of about 400 times the earth-moon distance. Estimate the ratio of sun-earth diameters.
Advertisements
Solution
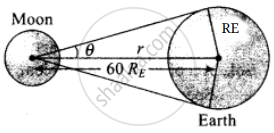
a. As the distance between moon and earth is greater than the radius of the earth, then radius of the earth can be treated as an arc.
According to the problem,
R, = length of arc
Distance between moon and earth = 60 RE
So, the angle subtended at distance r due to an arc of length `l` is
`θ_E = l/r = (2R_E)/(60 R_E) = 1/30` rad
= `1/30 xx 180^circ/pi` degree
= `6^circ/3.14` degree
= 1.9° ≈ 2°
Hence, the angle is subtended by the diameter of the earth 2θ = 2°.
b. According to the problem, the moon is seen as `(1/2)^circ` diameter from the earth and the earth is seen as 2° diameter from the moon.
As θ is proportional to diameter,
Hence, `"Diameter of earth"/"Diameter of moon" = 2/((1/2))` = 4
c. From parallax measurement given that the sun is at a distance of about 400 times the earth-moon distance, hence, `r_("sun")/r_("moon")` = 400
Sun and moon both appear to be of the same angular diameter as seen from the earth. (Suppose, here r stands for distance and D for diameter)
∴ `D_(sun)/r_(sun) = D_("moon")/r_("moon")`
⇒ `D_(sun)/D_("moon")` = 400
But `D_(earth)/D_("moon")` = 4
⇒ `D_(sun)/D_(earth)` = 100
APPEARS IN
RELATED QUESTIONS
The principle of ‘parallax’ in section 2.3.1 is used in the determination of distances of very distant stars. The baseline AB is the line joining the Earth’s two locations six months apart in its orbit around the Sun. That is, the baseline is about the diameter of the Earth’s orbit ≈ 3 × 1011m. However, even the nearest stars are so distant that with such a long baseline, they show parallax only of the order of 1” (second) of arc or so. A parsec is a convenient unit of length on the astronomical scale. It is the distance of an object that will show a parallax of 1” (second) of arc from opposite ends of a baseline equal to the distance from the Earth to the Sun. How much is a parsec in terms of meters?
Just as precise measurements are necessary in science, it is equally important to be able to make rough estimates of quantities using rudimentary ideas and common observations. Think of ways by which you can estimate the following (where an estimate is difficult to obtain, try to get an upper bound on the quantity):
the number of strands of hair on your head
Write true or false.
Every measurement involves two things – a number and a unit.
What are the S.I. units of
- mass
- length
- time and
- temperature.
Write their names and symbols.
Match the following.
| Column A | Column B |
| (1) Length | a. kilogram |
| (2) Mass | b. cubic metre |
| (3) Area | c. metre |
| (4) Volume | d. square metre |
Match the following.
| 1. | Length of the fore arm | metre |
| 2. | SI unit of length | second |
| 3. | Nano | 103 |
| 4. | SI Unit of time | 10–9 |
| 5. | Kilo | Cubit |
Have you seen frogs? Where? How many different types of frogs have you seen? Are all the frogs of the same length? Here are two interesting examples.
Arbaz plans to tile his kitchen floor with green square tiles. Each side of the tile is 10 cm. His kitchen is 220 cm in length and 180 cm wide. How many tiles will he need?
The fencing of a square garden is 20 m in length. How long is one side of the garden?
Chumki, Jhumri, and Imran need wire to make a fence.
- How much wire in all will the three need?
There are two beautiful lakes near a village. People come for boating and picnics in both the lakes. The village Panchayat is worried that with the noise of the boats the birds will stop coming. The Panchayat wants motorboats in only one lake. The other lake will be saved for the birds to make their nests.
- How many cm is the length of the boundary of lake A in the drawing?(use thread to find out)
There are two beautiful lakes near a village. People come for boating and picnics in both the lakes. The village Panchayat is worried that with the noise of the boats the birds will stop coming. The Panchayat wants motorboats in only one lake. The other lake will be saved for the birds to make their nests.
- How many kilometers long is the actual boundary of lake B?
There are two beautiful lakes near a village. People come for boating and picnics in both the lakes. The village Panchayat is worried that with the noise of the boats the birds will stop coming. The Panchayat wants motorboats in only one lake. The other lake will be saved for the birds to make their nests.
- A longer boundary around the lake will help more birds to lay their eggs. So which lake should be kept for birds? Which lake should be used for boats?
Give some examples of larger length measures.
SI unit of electric current is ______.
To measure the distance of a planet from the earth, ______ method is used.
