Question

The edge lengths of the unit cells in terms of the radius of spheres constituting fcc, bcc and simple cubic unit cell are respectively ______.

Options

• `2sqrt(2)r, (4r)/sqrt(3), 2r`

• `(4r)/sqrt(3), 2sqrt(2)r, 2r`

• `2r, 2sqrt(2)r, (4r)/sqrt(3)`

• `2r, (4r)/sqrt(3), 2sqrt(2)r`

Answer 1

The edge lengths of the unit cells in terms of the radius of spheres constituting fcc, bcc and simple cubic unit cell are respectively `2sqrt(2)r, (4r)/sqrt(3), 2r`.

Explanation:

Note: Distance between two atoms is always measured from their centres

(i) If the crystal lattice consists of SCC, the atom which is present at the comers touch each other

(ii) In case of FCC, atom present at the comer and the centre of the face touch each other.

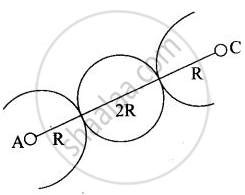
(iii) In case of BCC atom present at the corner and center of the body touch each other

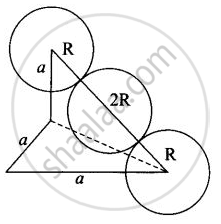
Edge length for different types of unit cells can be tabulated as

Type of Unit cell	Edge length
fcc	`2sqrt(2)r`
bcc	`4/sqrt(3)r`
scc	2r