Advertisements
Advertisements
Question
The figure shows three infinitely long straight parallel current carrying conductors. Find the
(i) magnitude and direction of the net magnetic field at point A lying on conductor 1,
(ii) magnetic force on conductor 2.

Solution
(i) Magnetic field due to a straight infinite long straight wire carrying current is given by
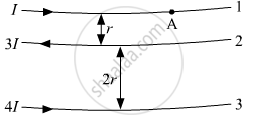
Current in wire 2 is 3I
\[B_2 = \frac{\mu_o}{4\pi}\frac{2 \times 3 I}{r}\]
\[ B_2 = \frac{\mu_o}{4\pi}(\frac{6 I}{r})\]
\[\text { The direction of magnetic field at point A due to wire 2 is in inward direction } . \]
Magnetic field (B3) at point A due to charge carrying wire 3
Current in wire 3 is 4I
\[B_3 = \frac{\mu_o}{4\pi}\frac{2 \times 4 I}{r + 2r}\]
\[ B_3 = \frac{\mu_o}{4\pi}(\frac{8 I}{3r})\]
\[\text { The direction of magnetic field at point A due to wire 3 is in the outward direction } . \]
\[\text { Net Magnetic field at point A }\]
\[B = B_2 - B_3 \]
\[ = \frac{\mu_o}{4\pi}(\frac{3 I}{r}) - \frac{\mu_o}{4\pi}(\frac{8 I}{3r})\]
\[ = \frac{\mu_o}{4\pi}(\frac{I}{3r}) \]
\[\text { The direction of net magnetic field at point A is in inward direction } . \]
(ii)
Magnitude of force on wire 2 due to wire 1
\[F_{21} = \frac{\mu_o}{4\pi} \frac{2 I_2 I_1}{r}\]
\[ = \frac{\mu_o}{4\pi}\frac{2 \times 3I \times I}{r} = \frac{\mu_o}{4\pi}\frac{6 I^2}{r}\]
\[\text { Magnitude of force on wire 2 due to wire } 3\]
\[ F_{23} = \frac{\mu_o}{4\pi} \frac{2 I_2 I_3}{r}\]
\[ = \frac{\mu_o}{4\pi}\frac{2 \times 3I \times 4I}{2r} = \frac{\mu_o}{4\pi}\frac{12 I^2}{r}\]
\[\text { Net force on wire 2 } = F_{23} - F_{21} \]
\[ = \frac{\mu_o}{4\pi}\frac{12 I^2}{r} - \frac{\mu_o}{4\pi}\frac{6 I^2}{r}\]
\[ = \frac{\mu_o}{4\pi}\frac{6 I^2}{r}\]
APPEARS IN
RELATED QUESTIONS
How does one understand this motional emf by invoking the Lorentz force acting on the free charge carriers of the conductor? Explain.
Two long and parallel straight wires A and B carrying currents of 8.0 A and 5.0 A in the same direction are separated by a distance of 4.0 cm. Estimate the force on a 10 cm section of wire A.
Derive the expression for force per unit length between two long straight parallel current carrying conductors. Hence define one ampere.
A long, straight wire carries a current along the z-axis, One can find two points in the x−y plane such that
(a) the magnetic fields are equal
(b) the directions of the magnetic fields are the same
(c) the magnitudes of the magnetic fields are equal
(d) the field at one point is opposite to that at the other point.
A long, straight wire carries a current i. Let B1 be the magnetic field at a point P at a distance d from the wire. Consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the section B2 be the magnetic field at this point due to this second only. Find the value of d/l so that B2 differs from B1 by 1%.
Two parallel wires separated by a distance of 10 cm carry currents of 10 A and 40 A along the same direction. Where should a third current by placed so that it experiences no magnetic force?
Equal currents are passing through two very long and straight parallel wires in the same direction. They will ______
Do magnetic forces obey Newton’s third law. Verify for two current elements dl1 = dlî located at the origin and dl2 = dlĵ located at (0, R, 0). Both carry current I.
Five long wires A, B, C, D and E, each carrying current I are arranged to form edges of a pentagonal prism as shown in figure. Each carries current out of the plane of paper.
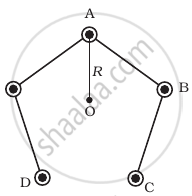
- What will be magnetic induction at a point on the axis O? AxisE is at a distance R from each wire.
- What will be the field if current in one of the wires (say A) is switched off?
- What if current in one of the wire (say) A is reversed?
Two long straight parallel current-carrying conductors are kept ‘a’ distant apart in the air. The direction of current in both the conductors is the same. Find the magnitude of force per unit length and the direction of the force between them. Hence define one ampere.
