Advertisements
Advertisements
Question
The gravitational force between a hollow spherical shell (of radius R and uniform density) and a point mass is F. Show the nature of F vs r graph where r is the distance of the point from the centre of the hollow spherical shell of uniform density.
Solution
Let us consider the diagram of a spherical shell having uniform density (ρ).
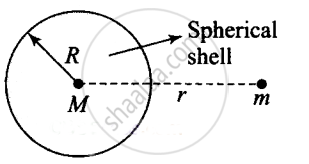
Mass of the shell = (Density) × (Volume)
`M = (ρ) xx 4/3 πR^3`
Therefore, the gravitational force between the hollow shell and point mass is`F = (GMm)/r^2` where M is the mass of the hollow spherical shell and m is the mass of point mass.
Therefore, the mass is distributed on the surface of the sphere only, then F = 0 for 0 < r < R (i.e., force inside the shell is zero)
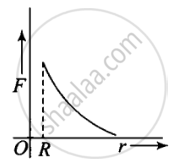
And `F = (GM)/r^2 for `r ≥ R`
The variation of F versus r is shown in the diagram. Force is maximum at the surface of shell and it is zero if r tends to infinity.
APPEARS IN
RELATED QUESTIONS
Let V and E be the gravitational potential and gravitational field at a distance r from the centre of a uniform spherical shell. Consider the following two statements :
(A) The plot of V against r is discontinuous.
(B) The plot of E against r is discontinuous.
Consider a planet moving in an elliptical orbit round the sun. The work done on the planet by the gravitational force of the sun
(a) is zero in any small part of the orbit
(b) is zero in some parts of the orbit
(c) is zero in one complete revolution
(d) is zero in no part of the motion.
Define one Newton. How much maximum acceleration can it produce in a mass of 1 kg?
Distinguish between gravity and gravitation
What is meant by the equation :
`g= Gxxm/r^2`
where the symbols have their usual meanings.
What does a force do in the following case?
You catch a kicked ball.
You can change the direction in which an object is moving by___________.
Explain the difference between g and G.
Law of gravitation gives the gravitational force between
Three uniform spheres, each having mass m and radius r, are kept in such a way that each touches the other two. The magnitude of the gravitational force on any sphere due to the other two is
