Question

The hypotenuse of a right angled triangle is 3`sqrt(5)`. If the smaller side is tripled and the larger side is doubled, the new hypotenuse will be 15 cm. Find the length of each side.

Answer 1

Let the smaller side of the right triangle be x cm and the longer side by y cm.
Using Pythagoras theorem, we have
x² + y² = `(3sqrt(5))^2`
⇒ x² + y² = 45    ...(i)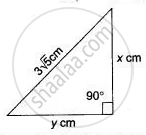

If the smaller side is tripled and larger side is doubled, then
The smaller side = 3x cm
Larger side = 2y cm
New hypotenuse = 15 cm
Then by Pythagoras theorem, we have
(3x)² + (2y)² = (15)²
⇒ 9x² + 4y² = 225   ...(ii)
From (i), y2 = 45 - x2 and putting in (ii) we get
9x² + 4(45 - x²) = 225
⇒ 9x² + 180 - 4x² = 225
⇒ 5x² = 225 - 180 = 45
⇒ x² = 9
⇒ x = ±3.
But x = -3 is not possible as length can't be - ve. Then x = 3 cm
From (i), we have
x² + y² = 45
⇒ 9 + y² = 45
⇒ y² = 36
⇒ y = ±6
Rejecting - ve sign then y = 6
Hence, the length of the smaller side = 3 cm
The length of the longer side = 6 cm.