Advertisements
Advertisements
Question
The lengths of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall?
Solution
In a triangle, the sum of the lengths of either two sides is always greater than the third side and also, the difference of the lengths of either two sides is always less than the third side. Here, the third side will be less than the sum of these two (i.e., 12 + 15 = 27) and also, it will be greater than the difference of these two (i.e., 15 − 12 = 3). Therefore, those two measures are 27cm and 3 cm.
APPEARS IN
RELATED QUESTIONS
Is it possible to have a triangle with the following sides?
6 cm, 3 cm, 2 cm
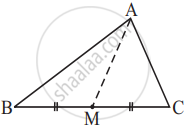
AM is a median of a triangle ABC.
Is AB + BC + CA > 2 AM?
(Consider the sides of triangles ΔABM and ΔAMC.)
ABCD is quadrilateral.
Is AB + BC + CD + DA < 2 (AC + BD)?
The sides of a triangle have lengths (in cm) 10, 6.5 and a, where a is a whole number. The minimum value that a can take is ______.
In ∆PQR, ______.
In ∆ABC ______.
Which of the following can be the length of the third side of a triangle whose two sides measure 18 cm and 14 cm?
Sum of two sides of a triangle is greater than or equal to the third side.
Sum of any two angles of a triangle is always greater than the third angle.
If the areas of two rectangles are same, they are congruent.
