Advertisements
Advertisements
Question
AM is a median of a triangle ABC.
Is AB + BC + CA > 2 AM?
(Consider the sides of triangles ΔABM and ΔAMC.)
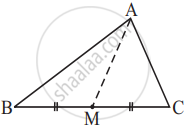
Solution
In a triangle, the sum of the lengths of either two sides is always greater than the third side.
In ΔABM,
AB + BM > AM ...(i)
Similarly, in ΔACM,
AC + CM > AM ...(ii)
Adding equation (i) and (ii),
AB + BM + MC + AC > AM + AM
AB + BC + AC > 2AM
Yes, the given expression is true.
APPEARS IN
RELATED QUESTIONS
ABCD is quadrilateral.
Is AB + BC + CD + DA < 2 (AC + BD)?
The lengths of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall?
The lengths of two sides of a triangle are 6 cm and 8 cm. Between which two numbers can the length of the third side fall?
The sides of a triangle have lengths (in cm) 10, 6.5 and a, where a is a whole number. The minimum value that a can take is ______.
In ∆PQR ______.
In ∆PQR, ______.
Which of the following can be the length of the third side of a triangle whose two sides measure 18 cm and 14 cm?
Sum of two sides of a triangle is greater than or equal to the third side.
The difference between the lengths of any two sides of a triangle is smaller than the length of third side.
Sum of any two angles of a triangle is always greater than the third angle.
