Advertisements
Advertisements
Question
ABCD is quadrilateral.
Is AB + BC + CD + DA < 2 (AC + BD)?
Solution
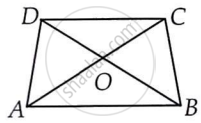
In a triangle, the sum of the lengths of either two sides is always greater than the third side.
Considering ΔOAB,
OA + OB > AB ...(i)
In ΔOBC,
OB + OC > BC ...(ii)
In ΔOCD,
OC + OD > CD ...(iii)
In ΔODA,
OD + OA > DA ...(iv)
Adding equations (i), (ii), (iii) and (iv), we obtain
OA + OB + OB + OC + OC + OD + OD + OA > AB + BC + CD + DA
2OA + 2OB + 2OC + 2OD > AB + BC + CD + DA
2OA + 2OC + 2OB + 2OD > AB + BC + CD + DA
2(OA + OC) + 2(OB + OD) > AB + BC + CD + DA
2(AC) + 2(BD) > AB + BC + CD + DA
2(AC + BD) > AB + BC + CD + DA
Yes, the given expression is true.
APPEARS IN
RELATED QUESTIONS
Is it possible to have a triangle with the following sides?
2 cm, 3 cm, 5 cm
Is it possible to have a triangle with the following sides?
3 cm, 6 cm, 7 cm
Is it possible to have a triangle with the following sides?
6 cm, 3 cm, 2 cm
Angles Q and R of a ΔPQR are 25° and 65°.
Write which of the following is true:

The sides of a triangle have lengths (in cm) 10, 6.5 and a, where a is a whole number. The minimum value that a can take is ______.
In ∆PQR ______.
In ∆ABC ______.
The length of two sides of a triangle are 7 cm and 9 cm. The length of the third side may lie between ______.
Sum of any two angles of a triangle is always greater than the third angle.
If the areas of two rectangles are same, they are congruent.
