Advertisements
Advertisements
Question
The magnetic flux passing through a coil perpendicular to its plane is a function of time and is given by OB = (2t3 + 4t2 + 8t + 8) Wb. If the resistance of the coil is 5 Ω, determine the induced current through the coil at a time t = 3 second.
Solution
Magnetic flux (ΦB) = (2t3 + 8t2 + 8t + 8)Wb
Resistance of the coil (R) = 5 Ω
time (t) = 3 second
Induced current through the coil, I = `"e"/"R"`
Induced emf, e = `("d"Φ_"B")/"dt" = "d"/"dt"` ((2t3 + 4t2 + 8t + 8) = 6t2 + 8t + 8
Here time (t) = 3 second
e = 6(3)2 + 8 × 3 + 8 = 54 + 24 + 8 = 86 V
∴ Induced current through the coil, I = `"e"/"R" = 86/5 = 17.2`A
APPEARS IN
RELATED QUESTIONS
What condition is necessary for the production of current by electromagnetic induction?
A light metal disc on the top of an electromagnet is thrown up as the current is switched on. Why? Give reason.
Draw a simple labeled diagram of a step-down transformer.
Find the odd one out and give its explanation.
Show that Lenz’s law is in accordance with the law of conservation of energy.
Obtain an expression for motional emf from Lorentz force.
A square coil of side 30 cm with 500 turns is kept in a uniform magnetic field of 0.4 T. The plane of the coil is inclined at an angle of 30° to the field. Calculate the magnetic flux through the coil.
An alternating emf of 0.2 V is applied across an L-C-R series circuit having R = 4Q, C = 80µF, and L = 200 mH. At resonance the voltage drop across the inductor is
A conducting bar of length L is free to slide on two parallel conducting rails as shown in the figure
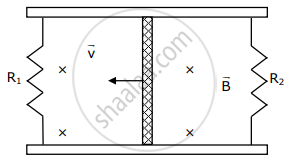
Two resistors R1 and R2 are connected across the ends of the rails. There is a uniform magnetic field `vec"B"` pointing into the page. An external agent pulls the bar to the left at a constant speed v. The correct statement about the directions of induced currents I1 and I2 flowing through R1 and R2 respectively is:
Show that for a given positive ion species in a cyclotron, (i) the radius of their circular path inside a dee is directly proportional to their speed, and (ii) the maximum ion energy achievable is directly proportional to the square of the magnetic induction.
