Advertisements
Advertisements
Question
The measures of two supplementary angles are (3x + 15)° and (2x + 5)°. Find x.
Solution
We know that, sum of two supplementary angles = 180°
∴ (3x + 15)° + (2x + 5)° = 180° ‘
3x + 15 + 2x + 5 = 180°
⇒ 3x + 2x+15 + 5 = 180°
⇒ 5x°+ 20° = 180°
⇒ 5x = 180° – 20°
⇒ 5x= 160°
⇒ x = `160/5`
⇒ x = 32°
APPEARS IN
RELATED QUESTIONS
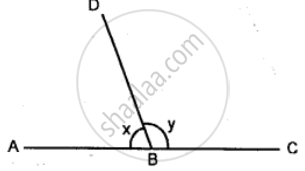
In the given diagram, ABC is a straight line. If x = 53°, find y.
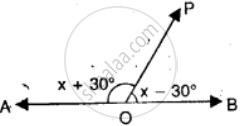
In the given figure, AOB is a straight line. Find the value of x and also answer each of the following:
(i) ∠AOP = ……..
(ii) ∠BOP = ……..
(iii) which angle is obtuse?
(iv) which angle is acute?
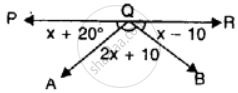
In the given figure, PQR is a straight line. Find x. Then complete the following:
(i) ∠AQB = _______
(ii) ∠BQP = _______
(iii) ∠AQR = _______
Write the complement angle of: `2/5` of 70°
`3/4` of 160°
Find the angle that is equal to its supplement?
Two supplementary angles are in the ratio 7 : 11. Find the angles.
For an angle x°, find:
(i) the complementary angle
(ii) the supplementary angle
(iii) the value of x° if its supplementary angle is three times its complementary angle.
Explain what do you understand by supplementary angles?
An angle is one-thirds of a straight line angle; find:
(i) the angle
(ii) the complement and the supplement of the angle obtained above.
