Advertisements
Advertisements
Question
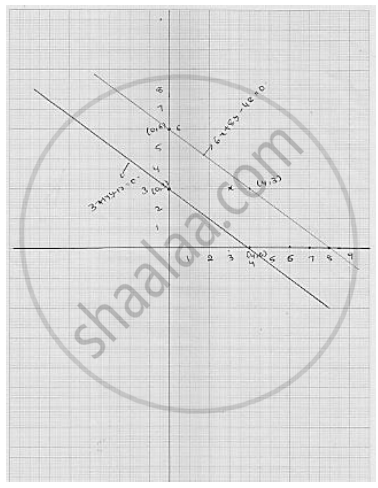
The path of a train A is given by the equation 3x + 4y − 12 = 0 and the path of another train
B is given by the equation 6x + 8y − 48 = 0. Represent this situation graphically.
Solution
We have
3x + 4y - 12 = 0
⇒ 3x = 12 - 4y
⇒ `3x = ( 12 - 4y ) /3 `
Putting y = 0 We get ` x (12 - 4 xx 0 ) /3= 4 `
Putting y = 3 , we get ` x = (12 - 4 xx 0 ) / 3 = 0 `
Thus, we have the following table for the points on the line 3x + 4y - 12 = 0
| x | 4 | 0 |
| y | 0 | 3 |
We have
6x + 8y - 48 = 0
6x + 8y = 48
6x = 48 - 8y
`x = 48 - (8y )/ 6 `
Putting y = 6 , we get ` x = ( 48 - 8 xx 6) / 6 = 0`
Putting y = 4 we get ` x = (48 - 8 xx 3) / 6= 4`
Thus, we have the following table for the points on the line 6x + 8y - 48 = 0
| x | 0 | 4 |
| y | 6 | 3 |
shaalaa.com
Linear Equation in Two Variables
Is there an error in this question or solution?
