Advertisements
Advertisements
Question
The radii of internal and external surfaces of a hollow spherical shell are 3 cm and 5 cm, respectively. It is melted and recast into a solid cylinder of diameter 14 cm. Find the height of the cylinder.
Solution
We have,
the internal base radius of spherical shell, r1 = 3 cm,
the external base radius of spherical shell, r2 = 5 cm and
the base radius of solid cylinder , r = 14/2 = 7 "cm".
Let the height of the cylinder be h.
As,
Volume of solid cylinder = volume of spherical shell
`rArr pir^2h = 4/3 pir_2^3 - 4/3pir_1^3`
`rArr pir^2h = 4/3pi(r_2^3 - r_1^3)`
`rArr r^2h =4/3 (r_2^3 - r_1^3)`
`rArr 7xx7xxh = 4/3(5^3-3^3)`
`rArr 49xx h =4/3(125-27)`
`rArr h = 4/3xx98/49`
`therefore h = 8/3 "cm"`
So, the height of the cylinder is `8/3` cm.
APPEARS IN
RELATED QUESTIONS
50 circular plates each of diameter 14cm and thickness 0.5cm are placed one above other to form a right circular cylinder. Find its total surface area?
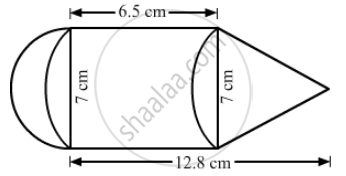
The adjoining figure represents a solid consisting of a cylinder surmounted by a cone at one end and a hemisphere at the other. Find the volume of the solid.
The radii of two cylinders are in the ratio of 2 : 3 and their heights are in the ratio of 5 : 3. Find the ratio of their volumes.
A cylinder with base radius 8 cm and height 2 cm is melted to form a cone of height 6 cm. Calculate the radius of the base of the cone.
Two cubes each of volume 125 cm3 are joined end to end to form a solid. Find the surface area of the resulting cuboid.
How many bricks, each measuring (25 cm × 11.25 cm × 6 cm), will be required to construct a wall (8 m × 6 m × 22.5 cm)?
The volumes of two cubes are in the ratio 1 : 27. The ratio of their surface area is
The diameter of a sphere is 14 cm. Its volume is
A hemispherical bowl of internal diameter 30 cm is full of a liquid. This liquid is poured into cylindrical bottles of diameter 5 cm and height 6 cm each. How many bottles are required?
A pen stand made of wood is in the shape of a cuboid with four conical depressions and a cubical depression to hold the pens and pins, respectively. The dimension of the cuboid are 10 cm, 5 cm and 4 cm. The radius of each of the conical depressions is 0.5 cm and the depth is 2.1 cm. The edge of the cubical depression is 3 cm. Find the volume of the wood in the entire stand.
