Advertisements
Advertisements
Question
The radius of a circle is 8 cm and the length of one of its chords is 12 cm. Find the distance of the chord from the centre.
Solution
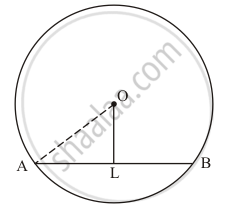
Radius of circle (OA) = 8 cm ......(Given)
Chord (AB) = 12cm .......(Given)
Draw a perpendicular OC on AB.
We know, perpendicular from centre to chord bisects the chord
Which implies, AC = BC = `12/2` = 6 cm
In right ΔOCA:
Using Pythagoras theorem,
OA2 = AC2 + OC2
64 = 36 + OC2
OC2 = 64 – 36 = 28
or OC = √28 = 5.291 (approx.)
The distance of the chord from the centre is 5.291 cm.
APPEARS IN
RELATED QUESTIONS
Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
In the given figure, A, B and C are three points on a circle with centre O such that ∠BOC = 30° and ∠AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.

Fill in the blank:
The longest chord of a circle is a ................of the circle.
Two chords AB, CD of lengths 5 cm, 11 cm respectively of a circle are parallel. If the distance between AB and CD is 3 cm, find the radius of the circle.
Let C be the mid-point of an arc AB of a circle such that m \[ \stackrel\frown{AB}\] = 183°. If the region bounded by the arc ACB and the line segment AB is denoted by S, then the centre O of the circle lies
If A and B are two points on a circle such that m \[ \stackrel\frown{AB}\] = 260°. A possible value for the angle subtended by arc BA at a point on the circle is
If A , B, C are three points on a circle with centre O such that ∠AOB = 90° and ∠BOC = 120°, then ∠ABC =
AB and CD are two parallel chords of a circle with centre O such that AB = 6 cm and CD= 12 cm. The chords are on the same side of the centre and the distance between them is 3 cm. The radius of the circle is
