Advertisements
Advertisements
Question
The sum and product of the zeros of a quadratic polynomial are \[- \frac{1}{2}\] and −3 respectively. What is the quadratic polynomial.
Solution
Let sum of quadratic polynomial is `a + ß = (-1)/2`
Product of the quadratic polynomial is `a ß = -3`
Let S and P denote the sum and product of the zeros of a polynomial as `(-1)/2 `and -3 .
Then
The required polynomial `g(x)` is given by
`g(x)=k (x^2-Sx +p)`
`=k[x^2-((-1)/2)x+(-3)]`
`= k [x^2+1/2x-3]`
Hence, the quadratic polynomial is `g(x)=k (x^2+x/2-3)`, where k is any non-zero real number
APPEARS IN
RELATED QUESTIONS
Classify the following polynomials as linear, quadratic, cubic and biquadratic polynomials:
`x+x^2 +4`
Classify the following polynomials as linear, quadratic, cubic and biquadratic polynomials:
`3x-2`
In Fig. 2.17, the graph of a polynomial p(x) is given. Find the zeros of the polynomial.
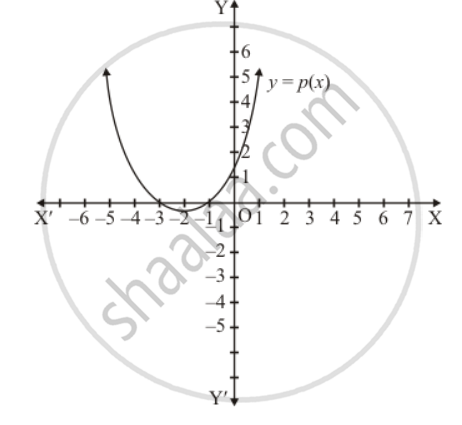
If Q.No. 14, c =
Divide. Write the quotient and the remainder.
(5x3 − 3x2) ÷ x2
Identify the following expression is polynomial. If not give reason:
`1/x^2 + 3x - 4`
Given that two of the zeroes of the cubic poly-nomial ax3 + bx2 + cx + d are 0, the third zero is ______.
Determine the degree of the following polynomial:
x3 – 9x + 3x5
Classify the following as a constant, linear, quadratic and cubic polynomials:
t2
Classify the following as a constant, linear, quadratic and cubic polynomials:
`sqrt(2)x - 1`
