Advertisements
Advertisements
Question
The variation of quantity A with quantity B, plotted in figure describes the motion of a particle in a straight line.
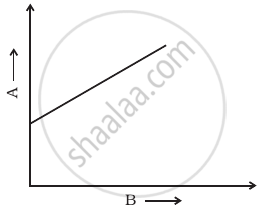
- Quantity B may represent time.
- Quantity A is velocity if motion is uniform.
- Quantity A is displacement if motion is uniform.
- Quantity A is velocity if motion is uniformly accelerated.
Solution
a, c, d
Explanation:
When we are calculating the velocity of a displacement-time graph we have to take the slope similarly we have to take the slope of a velocity-time graph to calculate acceleration. When the slope is constant motion will be uniform.
When we are representing motion by a graph it may be displacement-time, velocity-time or acceleration-time hence. B may represent time. For uniform motion, the velocity-time graph should be a straight line parallel to the time axis. For uniform motion velocity is constant hence, the slope will be positive. Hence quantity A is displacement.
For uniformly accelerated motion slope will be positive and A will represent velocity.
APPEARS IN
RELATED QUESTIONS
The speed-time graph of a particle moving along a fixed direction is shown in Fig. 3.28. Obtain the distance traversed by the particle between (a) t = 0 s to 10 s, (b) t = 2 s to 6 s.
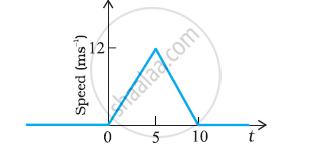
What is the average speed of the particle over the intervals in (a) and (b)
The velocity-time graph of a particle in one-dimensional motion is shown in Figure
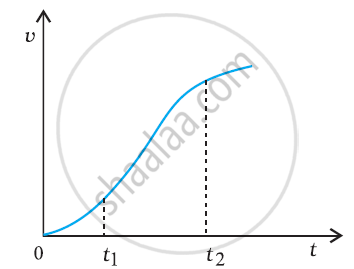
Which of the following formulae are correct for describing the motion of the particle over the time-interval t2 to t1?
(a) x(t2) = x(t1) + v(t1)(t2–t1) + (1/2)a(t2–t1)2
(b) v(t2)= v(t1) + a(t2–t1)
(c) vAverage = (x(t2) – x(t1)) / (t2 – t1)
(d) aAverage = (v(t2) – v(t1)) / (t2 – t1)
(e) x(t2) = x(t1) + vAverage(t2 – t1) + (1/2)aAverage(t2 – t1)2
(f) x(t2) – x(t1) = area under the v–t curve bounded by the t-axis and the dotted line shown.
Two particles A and B start from rest and move for equal time on a straight line. The particle A has an acceleration a for the first half of the total time and 2a for the second half. The particle B has an acceleration 2a for the first and a for the second half. Which particle has covered larger distance?
A player hits a baseball at some angle. The ball goes high up in space. The player runs and catches the ball before it hits the ground. Which of the two (the player or the ball) has greater displacement?
The increase in the speed of a car is proportional to the additional petrol put into the engine. Is it possible to accelerate a car without putting more petrol or less petrol into the engine?
Rain is falling vertically. A man running on the road keeps his umbrella tilted but a man standing on the street keeps his umbrella vertical to protect himself from the rain. But both of them keep their umbrella vertical to avoid the vertical sun-rays. Explain.
In figure shows the displacement-time graph of a particle moving on the X-axis.
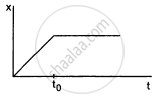
A particle has a velocity u towards east at t = 0. Its acceleration is towards west and is constant. Let xA and xB be the magnitude of displacements in the first 10 seconds and the next 10 seconds
A person travelling on a straight line moves with a uniform velocity v1 for a distance x and with a uniform velocity v2 for the next equal distance. The average velocity v is given by
