Advertisements
Advertisements
Question
The wavelength of a photon needed to remove a proton from a nucleus which is bound to the nucleus with 1 MeV energy is nearly ______.
Options
1.2 nm
1.2 × 10–3 nm
1.2 × 10–6 nm
1.2 × 101 nm
Advertisements
Solution
The wavelength of a photon needed to remove a proton from a nucleus which is bound to the nucleus with 1 MeV energy is nearly `underline(1.2 xx 10^-3 nm)`.
Explanation:
According to Einstein’s quantum theory light propagates in the bundles (packets or quanta) of energy, each bundle is called a photon and possessing energy. Energy of photon is given by
`E = hv = (hc)/λ`; where c = Speed of light, h = Planck's constant = `6.6 xx 10^-34` J-sec, v = Frequency in Hz, λ = the minimum wavelength of the photon required to eject the proton from nucleus.
In electron volt, `E(eV) = (hc)/(eλ) = 12375/(λ(Å)) = 12400/(λ(Å))`
According to the problem,
Energy of a photon, E = 1 MeV or 106 eV
Now, hc = 1240 eV nm
Now, `E = (hc)/λ`
⇒ λ = `(hc)/E = 1240/10^6` nm
= 1.24 × 10–3 nm
APPEARS IN
RELATED QUESTIONS
In an experiment on the photoelectric effect, the slope of the cut-off voltage versus the frequency of incident light is found to be 4.12 × 10−15 Vs. Calculate the value of Planck’s constant.
The work function for a certain metal is 4.2 eV. Will this metal give photoelectric emission for incident radiation of wavelength 330 nm?
In an accelerator experiment on high-energy collisions of electrons with positrons, a certain event is interpreted as annihilation of an electron-positron pair of total energy 10.2 BeV into two γ-rays of equal energy. What is the wavelength associated with each γ-ray? (1BeV = 109 eV)
Plot a graph showing the variation of photoelectric current with collector plate potential at a given frequency but for two different intensities I1 and I2, where I2 > I1.
Define the terms (i) ‘cut-off voltage’ and (ii) ‘threshold frequency’ in relation to the phenomenon of photoelectric effect.
Using Einstein’s photoelectric equation shows how the cut-off voltage and threshold frequency for a given photosensitive material can be determined with the help of a suitable plot/graph.
The frequency and intensity of a light source are doubled. Consider the following statements.
(A) The saturation photocurrent remains almost the same.
(B) The maximum kinetic energy of the photoelectrons is doubled.
The electric field at a point associated with a light wave is `E = (100 "Vm"^-1) sin [(3.0 xx 10^15 "s"^-1)t] sin [(6.0 xx 10^15 "s"^-1)t]`.If this light falls on a metal surface with a work function of 2.0 eV, what will be the maximum kinetic energy of the photoelectrons?
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
A monochromatic light source of intensity 5 mW emits 8 × 1015 photons per second. This light ejects photoelectrons from a metal surface. The stopping potential for this setup is 2.0 V. Calculate the work function of the metal.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
A small metal plate (work function φ) is kept at a distance d from a singly-ionised, fixed ion. A monochromatic light beam is incident on the metal plate and photoelectrons are emitted. Find the maximum wavelength of the light beam, so that some of the photoelectrons may go round the ion along a circle.
Consider the situation of the previous problem. Consider the faster electron emitted parallel to the large metal plate. Find the displacement of this electron parallel to its initial velocity before it strikes the large metal plate.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
Use Einstein’s photoelectric equation to show how from this graph,
(i) Threshold frequency, and (ii) Planck’s constant can be determined.
How does one explain the emission of electrons from a photosensitive surface with the help of Einstein’s photoelectric equation?
Choose the correct answer from given options
Photons of frequency v are incident on the surface of two metals A and B of threshold frequency 3/4 v and 2/3 v, respectively. The ratio of maximum kinetic energy of electrons emitted from A to that from B is
The minimum energy required to remove an electron is called ______.
- In the explanation of photo electric effect, we assume one photon of frequency ν collides with an electron and transfers its energy. This leads to the equation for the maximum energy Emax of the emitted electron as Emax = hν – φ0 where φ0 is the work function of the metal. If an electron absorbs 2 photons (each of frequency ν) what will be the maximum energy for the emitted electron?
- Why is this fact (two photon absorption) not taken into consideration in our discussion of the stopping potential?
A student performs an experiment on photoelectric effect, using two materials A and B. A plot of Vstop vs ν is given in Figure.
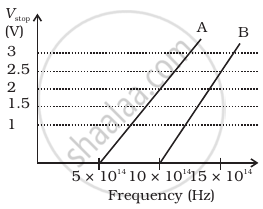
- Which material A or B has a higher work function?
- Given the electric charge of an electron = 1.6 × 10–19 C, find the value of h obtained from the experiment for both A and B.
Comment on whether it is consistent with Einstein’s theory:
A photon of wavelength 663 nm is incident on a metal surface. The work function of the metal is 1.50 eV. The maximum kinetic energy of the emitted photoelectrons is ______.
The photon emitted during the de-excitation from the first excited level to the ground state of a hydrogen atom is used to irradiate a photocathode in which the stopping potential is 5 V. Calculate the work function of the cathode used.
