Advertisements
Advertisements
Question
Three bells toll at intervals of 9, 12, 15 minutes. If they start tolling together, after what time will they next toll together?
Solution
Three bells toll at intervals of 9, 12 and, 15 minutes.
The time when they will toll together again is given by the LCM of 9, 12, and 15.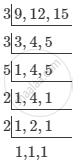
Required time = 22 × 32 × 5
= 180 minutes
=3 h
If they start tolling together, they will toll together again after 3 h.
APPEARS IN
RELATED QUESTIONS
9 8
+ 4 A
C B 3
Fill in the blanks:
For every number, its factors are ______ and its multiples are ______
Reduce each of the following fraction to the lowest term:
`161/207`
Reduce each of the following fraction to the lowest term:
`296/481`
There are 527 apples, 646 pears, and 748 oranges. These are to be arranged in heaps containing the same number of fruits. Find the greatest number of fruits possible in each heap. How many heaps are formed?
A rectangular courtyard is 18 m 72 cm long and 13 m 20 cm broad. It is to be paved with square tiles of the same size. Find the least possible number of such tiles.
Find the HCF of
Two consecutive numbers
Find the least number which when divided by 25, 40, and 60 leaves 9 as the remainder in each case.
Find the greatest number of five digits exactly divisible by 9, 12, 15, 18 and 24.
Now complete the table, for different numbers of bangles. For each number see what different groups can be made.
| Number of bangles | Different groups we can make |
| 18 | 1, 2, 3, 6, 9, 18 |
| 24 | 1, 2, .................... |
| 5 | |
| 9 | |
| 7 | |
| 2 | |
| 10 | |
| 1 | |
| 20 | |
| 13 | |
| 21 |
